Kongruenssi

Kongruenssin käsite mahdollistaa jaollisuuteen liittyvien asioiden käsittelyn tavalla, joka muistuttaa yhtälöiden käsittelyä.

Määritelmä. Olkoon m positiivinen kokonaisluku. Jos a,b ja a-b on jaollinen luvulla m sanotaan, että luku a on kongruentti luvun b kanssa modulo m, ja merkitään

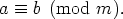
Tätä joukon relaatiota nimitetään kongruenssiksi ja luku m on sen moduli.

Edellisen vastakohta on, että luku a on epäkongruentti luvun b kanssa modulo m. Tätä merkitään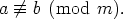

Esimerkki. 27 2 (mod 5), 12 -8 (mod 10),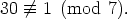

Määritelmän mukaan a b (mod m) jos ja vain jos a on luvun m monikertaa vaille yhtä suuri kuin b. Toisin sanoen

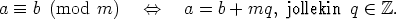
Tästä nähdään helposti (tarkistamalla ekvivalenssirelaation ehdot E1-E3), että kongruenssi modulo m on joukon ekvivalenssirelaatio.

Lause. (i) Jos a b (mod m) ja c d (mod m), niin

(ii) Jos ca cb (mod m) ja syt(c,m) = 1, niin a b (mod m).
(iii) Jos a b (mod km), missä k on positiivinen kokonaisluku, niin a b (mod m).

Todistus. (i) Luku (a + c) - (b + d) = (a - b) + (c - d) on jaollinen luvulla m, koska m | (a - b) ja m | (c - d). Samoin luku ac - bd = (a - b)c + (c - d)b on luvun m monikerta.

(ii) Koska c ja m ovat parittain suhteellisia alkulukuja ja m | (ca - cb) = c(a - b), niin m | (a - b) (katso aritmetiikan peruslausetta edeltävä lause).

(iii) Koska luku a - b on luvun km monikerta on se myös luvun m monikerta.

Lauseen kohdan (i) mukaan kongruensseja modulo m voi laskea yhteen ja kertoa puolittain, samoin voidaan myös vähentää ja korottaa potenssiin puolittain. Erityisesti, jos P(x) on kokonaiskertoiminen polynomi eli

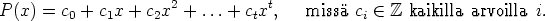
niin kongruenssista a b (mod m) seuraa, että P(a) P(b) (mod m).

Linkit:
Ekvivalenssirelaatio
Aritmetiikan peruslause
Jäännösluokka