smr055.html

Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003

LINEAARIALGEBRA

Lisää matriisitulosta

Lause. (Skalaarin siirto) Jos A = (a_ij)_n×m ja B = (b_ij)_m×p ovat matriiseja ja r on jokin reaaliluku, niin

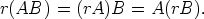
r(AB) = (rA)B = A(rB).

Todistus. Kirjoitetaan

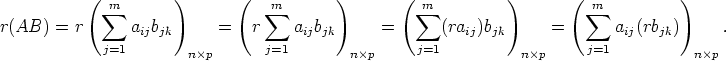
( sum m ) ( sum m ) ( m sum ) ( sum m ) r(AB)=r a b = r a b = (ra )b = a (rb ) . ij jk ij jk ij jk ij jk j=1 n× p j=1 n×p j=1 n×p j=1 n×p

Tässä toiseksi viimeinen matriisi on (rA)B ja viimeinen on A(rB).

Seuraava lause on helppo nähdä todeksi.

Lause. Kaikilla matriiseilla A = (a_ij)_n×m on

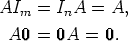Assosiatiivilain nojalla voidaan kolmen matriisin tulo kirjoittaa ilman sulkeita ABC ja yleisemmin monen matriisin tulo voidaan kirjoittaa A₁A₂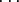A_k. Jos A on (n×n)-neliömatriisi, sen potenssi määritellään luonnollisella tavalla:

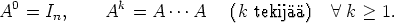
A0 = In, Ak = A ...A (k tekijää) A k > 1.

Silloin

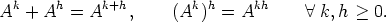
Ak + Ah = Ak+h, (Ak)h = Akh A k,h > 0.

Huomaa, että (AB)^k = ABAB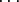AB, joka on yleensä eri matriisi kuin A^kB^k, kun k > 2.

Lause. (AB)^T = B^TA^T.

Todistus. Merkitään A = (a_ij)_n×m ja B = (b_ij)_m×p. Tällöin

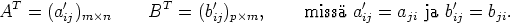
AT = (a'ij)m× n BT = (b'ij)p×m, miss ä a'ij = aji ja b'ij = bji.

Tulo B^T A^T on siis määritelty ja B^TA^T = (v_ij)_p×n, missä

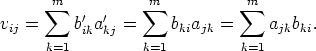
m m m sum ' ' sum sum vij = bika kj = bkiajk = ajkbki. k=1 k=1 k=1

Alkio v_ij on siis matriisin AB paikassa (j,i) oleva alkio.

Käyttämällä toistuvasti edellistä lausetta saadaan:

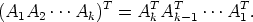
(A1A2 ...Ak)T = ATk ATk- 1...AT1.

Linkit:
Matriisitulo
Yksinkertaisia matriiseja
Matriisitulon ominaisuuksia