Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		RYHMÄ
 

Ryhmän perusominaisuuksia

Seuraava lause antaa käyttöön monesti tarvittavan ryhmän yhtälön supistussäännön.

Lause. Olkoon (G,*) ryhmä ja a,b,c (- G. Silloin

     (a)   jos a * b = a * c, niin b = c,
     (b)   jos b * a = c * a, niin b = c.

Todistus. Oletetaan, että a * b = a * c. Koska a on ryhmän alkio, on sillä käänteisalkio a-1. Silloin operoimalla tällä käänteisalkiolla oletuksen yhtälöä vasemmalta puolelta saadaan

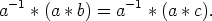
a- 1 * (a * b) = a-1 * (a *c).

Olkoon e ryhmän neutraalialkio. Neutraalialkion ominaisuuksien ja ryhmän assosiatiivisuuden nojalla saadaan

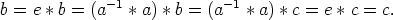
b = e * b = (a-1 *a) * b = (a-1 * a) *c = e *c = c.

Vastaavasti voidaan todistaa kohta (b). []

Edellisen lauseen perusteella voidaan yhtälöstä a * b = a * c supistaa molemmilta puolilta alkio a. Huomaa, että yhtälöstä a * b = c * a ei yleisesti voi poistaa alkiota a molemmilta puolilta, vain Abelin ryhmissä tämä on yleisesti mahdollista.

Lause. Ryhmässä (G,*) pätee:

     (i)  Ryhmän neutraalialkio e on yksikäsitteinen.
     (ii)  Jokaisella alkiolla a (- G on yksikäsitteinen käänteisalkio a-1.
     (iii)  Jos a (- G, niin (a-1)-1 = a.
     (iv)  Kaikilla a,b (- G : (a * b)-1 = b-1 * a-1.

Todistus. (i) Tehdään vastaoletus, että ryhmällä (G,*) on kaksi neutraalialkiota e ja e'. Silloin ehdon (G2) nojalla e = e * e' = e'.

Kohta (ii) on edellisen lauseen seuraus.

(iii) Käänteisalkion määritelmän mukaan on (a-1)-1 * a-1 = e. Toisaalta a * a-1 = e, joten käyttäen taas edellisen lauseen supistussääntöä saadaan, että (a-1)-1 = a.

(iv) Suoraan laskemalla saadaan (käyttäen assosiatiivisuutta):

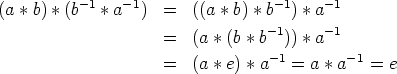
(a * b) * (b-1 * a- 1) = ((a * b) * b-1) * a-1 = (a * (b * b-1)) * a-1 - 1 -1 = (a * e) * a = a * a = e
Samoin todetaan, että (b-1 * a-1) * (a * b) = e, joten saadaan väite. []

Linkit:
Ryhmä