| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RYHMÄ |
Esimerkkejä aliryhmistä
Esimerkki.
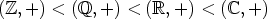
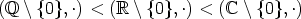
Esimerkki. Pari ( , +) on ryhmä. Merkitään jollekin kokonaisluvulle m > 1,
, +) on ryhmä. Merkitään jollekin kokonaisluvulle m > 1,
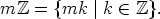
Osoitetaan käyttäen aliryhmäkriteeriä, että (m , +) on ryhmän (
, +) on ryhmän ( , +) aliryhmä.
, +) aliryhmä.
Selvästi joukko m on epätyhjä. Oletetaan, että a,b
on epätyhjä. Oletetaan, että a,b  m
m . Koska ryhmän binäärioperaatio on
yhteenlasku, on käänteisalkion b-1 tilalla nyt vasta-alkio -b. Merkintää a * b-1 vastaa siis
a + (-b) = a - b. Nyt joillekin kokonaisluvuille k1 ja k2 on a = mk1 ja b = mk2, joten
-b = m(-k2). Täten a - b = mk1 + m(-k2) = m(k1 - k2)
. Koska ryhmän binäärioperaatio on
yhteenlasku, on käänteisalkion b-1 tilalla nyt vasta-alkio -b. Merkintää a * b-1 vastaa siis
a + (-b) = a - b. Nyt joillekin kokonaisluvuille k1 ja k2 on a = mk1 ja b = mk2, joten
-b = m(-k2). Täten a - b = mk1 + m(-k2) = m(k1 - k2)  m
m , koska k1 - k2
, koska k1 - k2 
 . Siis
(m
. Siis
(m , +) < (
, +) < ( , +).
, +).
Esimerkki. Säännöllisten (n×n)-matriisien joukko GLn( ) = {A
) = {A  Mn×n(
Mn×n( ) | det(A)
) | det(A)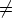 0} on
ryhmä matriisien kertolaskun suhteen. Näytetään, että joukon GLn(
0} on
ryhmä matriisien kertolaskun suhteen. Näytetään, että joukon GLn( ) osajoukko
) osajoukko
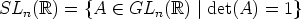
muodostaa aliryhmän. SLn( )
)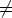 Ø, koska identiteettimatriisi In
Ø, koska identiteettimatriisi In  SLn(
SLn( ). Olkoon A,B
). Olkoon A,B  SLn(
SLn( ).
Silloin AB-1
).
Silloin AB-1  SL
n(
SL
n( ), koska det(AB-1) = det(A) det(B-1) = det(A) det(B)-1 = 1 . 1-1 = 1.
), koska det(AB-1) = det(A) det(B-1) = det(A) det(B)-1 = 1 . 1-1 = 1.
Esimerkki. Olkoon (G,*) mikä tahansa ryhmä ja merkitään
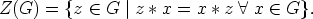
Osoitetaan, että (Z(G),*) on ryhmän (G,*) aliryhmä. Aliryhmää (Z(G),*) kutsutaan ryhmän (G, *) keskukseksi.
Olkoon e ryhmän (G,*) neutraalialkio. Koska e * a = a = a * e kaikilla a  G, on
joukko Z(G) epätyhjä. Oletetaan, että a,b
G, on
joukko Z(G) epätyhjä. Oletetaan, että a,b  Z(G). Osoitetaan ensin, että b-1
Z(G). Osoitetaan ensin, että b-1  Z(G).
Koska b
Z(G).
Koska b  Z(G), on kaikilla x
Z(G), on kaikilla x  G, b * x = x * b. Operoimalla tätä yhtälöä molemmin
puolin vasemmalta alkiolla b-1 ja käyttämällä assosiatiivisuutta nähdään, että
x = e * x = (b-1 * b) * x = b-1 * (b * x) = b-1 * (x * b). Operoimalla näin saatua yhtälöä
vastaavasti oikealta puolelta saadaan x * b-1 = (b-1 * x) * (b * b-1) = b-1 * x.
G, b * x = x * b. Operoimalla tätä yhtälöä molemmin
puolin vasemmalta alkiolla b-1 ja käyttämällä assosiatiivisuutta nähdään, että
x = e * x = (b-1 * b) * x = b-1 * (b * x) = b-1 * (x * b). Operoimalla näin saatua yhtälöä
vastaavasti oikealta puolelta saadaan x * b-1 = (b-1 * x) * (b * b-1) = b-1 * x.
Koska a, b-1  Z(G), saadaan käyttämällä assosiatiivisuutta, että
(a * b-1 ) * x = a * (b-1 * x) = a * (x * b-1) = (a * x) * b-1 = (x * a) * b-1 = x * (a * b-1). Täten
a * b-1
Z(G), saadaan käyttämällä assosiatiivisuutta, että
(a * b-1 ) * x = a * (b-1 * x) = a * (x * b-1) = (a * x) * b-1 = (x * a) * b-1 = x * (a * b-1). Täten
a * b-1  Z(G).
Z(G).
Linkit:
Aliryhmä
Esimerkkejä ryhmistä
Esimerkkejä ryhmistä 2
Yksinkertaisia matriiseja
Matriisitulon determinantti
Säännöllinen matriisi