Ryhmän generointi

Olkoon (G,*) ryhmä ja S joukon G jokin osajoukko. Tarkastellaan ryhmän (G,*) sellaisten aliryhmien (H,*) parvea, joissa S 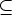H. Tämä parvi on epätyhjä, koska ainakin ryhmä (G,*) kuuluu siihen. Kuten sivun Huomioita aliryhmästä toisessa lauseessa todettiin on parven aliryhmien (H,*) leikkaus myös aliryhmä. Tätä leikkausta kutsutaan joukon S generoimaksi ryhmän (G,*) aliryhmäksi ja sitä merkitään symbolilla (< S >,*), missä siis

Joukon S alkioita sanotaan ryhmän (< S >,*) generaattoreiksi. Jos generaattoreita on äärellisen monta, toisin sanoen S = {a₁,...,a_k}, sanotaan, että ryhmä (< S >,*) on äärellisesti generoitu, ja käytetään merkintää

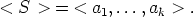
Määritelmän mukaan ryhmä (< S >,*) on pienin ryhmän (G,*) aliryhmä, jonka alkiojoukkoon S kuuluu. Tässä pienuus on ymmärrettävä sisältyvyytenä, tämä pienin joukko sisältyy kaikkiin muihin sellaisiin mahdollisiin joukkoihin, joissa S on osajoukkona ja jotka muodostavat ryhmän (G,*) aliryhmän.

Olkoon e neutraalialkio. Esimerkkinä huomaamme, että < Ø > = {e}, < e > = {e} ja jos (H,*) < (G,*), niin < H > = H.

Lause. Olkoon (G,*) ryhmä ja S 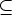G. Silloin

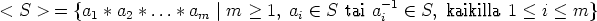
tai jos S = Ø, niin < S >= {e}, missä e on ryhmän G neutraalialkio.

Todistus. Jos S = Ø, tiedetään väite todeksi. Olkoon S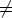Ø ja merkitään

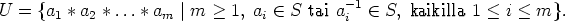
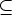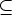Valitsemalla tulossa a₁ * a₂ * ... * a_m luvuksi m = 1 nähdään, että S U. Aliryhmäkriteeriä käyttämällä nähdään, että (U,*) < (G,*). Nimittäin, jos a₁ *a₂ *...*a_m U ja a₁'*a₂'*...*a_n' U, niin (a₁ * a₂ * ...*a_m) * (a₁'*a₂'*...*a_n')^-1 = a ₁ *a₂ *...*a_m * (a_n')^-1 *...* (a ₂')^-1 * (a ₁')^-1 U. Täten <  S  > U.

Toisaalta jokainen joukko H, joka esiintyy leikkauksessa (1), sisältää kaikki joukon U alkiot. Täten U 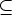<  S  > . Siis <  S  > = U.

Jos ryhmä (G,*) on äärellinen, edellisen lauseen kaava saa yksinkertaisemman muodon äärellisiä ryhmiä koskevan aliryhmäkriteerin muunnelman perusteella:

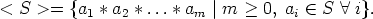
Esimerkki. Ääretön ryhmä (, +) on äärellisesti generoitu, sillä

Linkit:
Aliryhmä
Huomioita aliryhmästä