Esimerkkejä ryhmien homomorfialauseen käytöstä

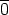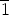Esimerkki. Palautetaan mieleen joukko _m = {,,...,}. Kuvaus

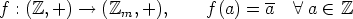
on homomorfismi, koska f(a + b) = 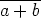= 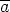+ 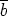= f(a) + f(b) kaikilla a,b . Ryhmän (_m, +) neutraalialkio on 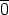. Täten ker(f) = {a | 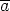= 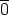} = {a Z | m | a} = m. Koska Im(f) = _m, on homomorfialauseen nojalla

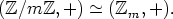
Kuten sivulla Esimerkkejä normaaleista aliryhmistä ja tekijäryhmistä on nyt luontevaa, että tekijäryhmän /m operaatio on +. Tämän isomorfismin antaa kuvaus F(a + m) = f(a) = 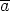kaikilla a _m.

Seuraavissa esimerkeissä tekijäryhmän operaatio  ^.  määritellään kuten sivun Tekijäryhmä lauseessa.

Esimerkki. Merkitään ^* = \{0} ja ₊ = {x | x > 0}. Kuvaus f : (^*, ^. ) ( ₊, ^. ), missä f(x) = |x| kaikilla x ^*, on homomorfismi, sillä f(xy) = |xy| = |x||y| = f(x)f(y). Koska ryhmän (₊, ^. ) neutraalialkio on 1, on kuvauksen ydin ker(f) = {x ^* ||x| = 1} = {±1}. Selvästi Im (f) = ₊. Täten homomorfialauseen nojalla kuvaus f indusoi isomorfismin

Huomaa, että a ^. {±1} = {±a} kaikilla a ^*.

Esimerkki. Kuvaus (vertaa sivuun Esimerkkejä aliryhmistä)

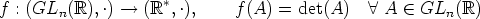
on homomorfismi, sillä f(AB) = det(AB) = det(A) det(B) = f(A) ^. f(B) kaikilla A, B GL_n ().

Ryhmän (^* ,  ^. ) neutraalialkio on 1, joten

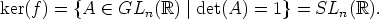
Koska Im (f) = ^* saadaan homomorfialauseen mukaan

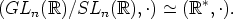
Esimerkki. Olkoon e ryhmän (G,*) neutraalialkio. Triviaali homomorfismi f : (G,*) (G,*), missä f(a) = e kaikilla a G, indusoi isomorfian

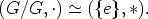
Identtinen kuvaus id:(G,*) (G,*), missä id(a) = a kaikilla a G, on homomorfismi ja se indusoi isomorfian

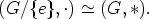
Linkit:
Esimerkkejä normaaleista aliryhmistä ja tekijäryhmistä
Tekijäryhmä
Ryhmien homomorfialause
Esimerkkejä aliryhmistä