| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | POLYNOMIRENKAAT |
Polynomirengas
Reaalikertoimiset polynomit a0 + a1x + 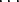 + anxn, missä a
i
+ anxn, missä a
i 
 kaikilla i = 1,...,n, ovat
tuttuja monesta yhteydestä. Olkoon (R, +, . ) rengas. Yleistetään polynomin käsitettä
korvaamalla polynomin kertoimet a0,...,an renkaan (R, +, . ) alkioilla. Tällaisten polynomien
yhteen- ja kertolasku voidaan suorittaa aivan kuten reaalisessakin tapauksessa, nyt kertoimiin
sovelletaan renkaan (R, +, . ) laskutoimituksia.
kaikilla i = 1,...,n, ovat
tuttuja monesta yhteydestä. Olkoon (R, +, . ) rengas. Yleistetään polynomin käsitettä
korvaamalla polynomin kertoimet a0,...,an renkaan (R, +, . ) alkioilla. Tällaisten polynomien
yhteen- ja kertolasku voidaan suorittaa aivan kuten reaalisessakin tapauksessa, nyt kertoimiin
sovelletaan renkaan (R, +, . ) laskutoimituksia.
Kaikkien yhden muuttujan x polynomien, joiden kertoimet kuuluvat renkaaseen (R, +, . ), joukosta käytetään merkintää R[x]. Siis
![R[x] = {a + a x + ...+ a xn | n > 0, a (- R, k = 1,...,n}.
0 1 n k](images/smr2801x.gif)
Joukon alkioita sanotaan polynomeiksi yli renkaan R (tai renkaan R suhteen).
Kaksi joukon R[x] polynomia
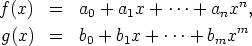
Olkoon f(x) = 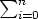 aixi
aixi  R[x] ja g(x) =
R[x] ja g(x) = 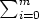 bixi
bixi  R[x]. Voidaan olettaa, että
m > n. Määritellään polynomien yli renkaan R yhteen- ja kertolasku seuraavasti:
R[x]. Voidaan olettaa, että
m > n. Määritellään polynomien yli renkaan R yhteen- ja kertolasku seuraavasti:
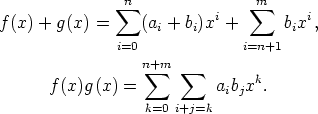 |
Lause. Olkoon (R, +, . ) rengas. Silloin R[x] on rengas yllä määriteltyjen operaatioiden + ja . suhteen. Lisäksi (R[x], +, . ) on kommutatiivinen jos ja vain jos (R, +, . ) on kommutatiivinen.
Todistus. Renkaan (R[x], +, . ) nolla-alkio on nollapolynomi 0
R ja sen ykkösalkio on
vakiopolynomi 1D = 1Dx0. Polynomin a(x) = a
0 + a1x + 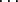 + anxn
+ anxn  R[x] vasta-alkio on
polynomi -a(x) = -a0 - a1x -
R[x] vasta-alkio on
polynomi -a(x) = -a0 - a1x -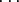 - anxn, missä -a
i on renkaan alkion ai vasta-alkio kaikilla
i = 0, ... , n. Sen toteamiseksi, että (R[x], +, . ) on tosiaan rengas on käytävä kaikki
rengaspostulaatit lävitse. Tehdään esimerkkinä assosiatiivisuuden todistaminen ja jätetään
muut harjoitukseksi.
- anxn, missä -a
i on renkaan alkion ai vasta-alkio kaikilla
i = 0, ... , n. Sen toteamiseksi, että (R[x], +, . ) on tosiaan rengas on käytävä kaikki
rengaspostulaatit lävitse. Tehdään esimerkkinä assosiatiivisuuden todistaminen ja jätetään
muut harjoitukseksi.
Olkoot polynomit a(x) = a0 + a1x + 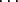 + anxn, b(x) = b
0 + b1x +
+ anxn, b(x) = b
0 + b1x + 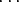 + bmxm ja
c(x) = c0 + c1 x +
+ bmxm ja
c(x) = c0 + c1 x + 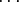 + ckxk joukon R[x] alkioita. Silloin käyttäen renkaan R assosiatiivisuutta
saadaan
+ ckxk joukon R[x] alkioita. Silloin käyttäen renkaan R assosiatiivisuutta
saadaan
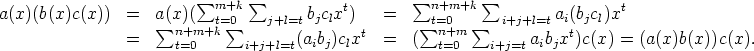
Lauseen loppuosa on ilmeinen. ![[]](images/msam10-c-3.gif)
Rengasta (R[x], +, . ) sanotaan polynomirenkaaksi yli renkaan R.
Linkit:
Rengas
Esimerkkejä polynomirenkaista