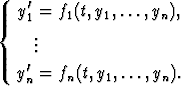
Normaalimuotoinen kertalukua n oleva differentiaaliyhtälöryhmä — esimerkiksi kertalukua n olevaa yhtälöä vastaava normaaliryhmä — on
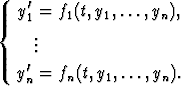
Tämän ratkaisu muodostuu n funktiosta y1(t), . . . , yn(t). Näiden voidaan katsoa määrittelevän käyrän n-ulotteisessa avaruudessa: jokaista riippumattoman muuttujan arvoa t vastaa käyrän piste, jonka koordinaatit ovat (y1(t), . . . , yn(t)). Avaruuden koordinaattiakseleilla ovat siis funktioiden yk arvot ja muuttuja t on käyräparametrin asemassa. Kyseessä on ratkaisun esitys faasiavaruudessa.
Jos yhtälöryhmä on autonominen, ts. muotoa
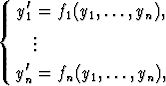
voidaan käyrän tangenttivektori laskea suoraan differentiaaliyhtälöryhmästä:
(y1 ' (t), . . . , yn'(t)) = (f1(y1, . . . , yn), . . . , fn(y1, . . . , yn)).
Faasiavaruuteen muodostuu siis suuntakenttä.
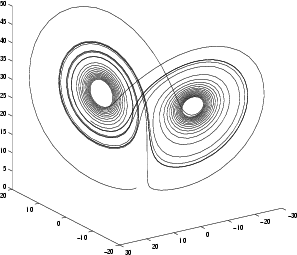
Jos n = 3, on yhtälöitä ja tuntemattomia funktioita kolme. Faasiavaruus on siis kolmiulotteinen ja ratkaisukäyrästä (y1(t), y2(t), y3(t)) voidaan piirtää kuvia projisioimalla kolmiulotteinen avaruus jollakin tavoin kaksiulotteiseen tasoon. Kyseessä voi olla projektio johonkin koordinaattitasoon tai ns. aksonometrinen kuva, projektio johonkin vinossa asennossa olevaan tasoon.
Jos n > 3, tilanne on periaatteessa samankaltainen, mutta faasiavaruuden projektiot kaksiulotteiseen tasoon kadottavat enemmän tietoa n-ulotteisen avaruuden tilanteesta. Luonnollisinta onkin tyytyä johonkin koordinaattitasoon otettuun projektioon. Esimerkiksi projektio y1y2-tasoon saadaan tarkastelemalla vain kahta ensimmäistä funktiota: (y1 (t), y2(t)).
Esimerkkinä on aksonometrinen kuva Lorenzin systeemin
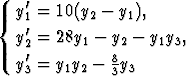
eräästä ratkaisukäyrästä kolmiulotteisessa faasiavaruudessa: