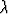 1 +
1 + 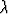 2ex +
2ex + 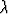 3x2 = 0
arvot x = 0, x = 1, x = -1 ja ratkaisemalla saatu lineaarinen yhtälöryhmä
3x2 = 0
arvot x = 0, x = 1, x = -1 ja ratkaisemalla saatu lineaarinen yhtälöryhmä
Kolmannen kertaluvun lineaarisella ja homogeenisella differentiaaliyhtälöllä
(x - 1)y''' - xy'' + y' = 0
on ilmeisestikin ratkaisuna vakiofunktio, esimerkiksi y1(x) = 1. Koska kerroinfunktioiden x - 1, -x ja 1 summa on = 0, on ratkaisuna myös eksponenttifunktio y2(x) = ex. Melko helposti on havaittavissa, että lisäksi funktio y3(x) = x2 toteuttaa yhtälön.
Lineaarista ja homogeenista yhtälöä koskeva teoria sanoo tällöin, että yhtälön yleinen ratkaisu saadaan näistä:
y = C1 + C2ex + C3x2.
Edellytyksenä on, että funktiot 1, ex ja x2 ovat lineaarisesti riippumattomia. Näin
kuitenkin on, mikä nähdään esimerkiksi sijoittamalla testiyhtälöön 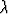 1 +
1 + 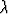 2ex +
2ex + 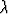 3x2 = 0
arvot x = 0, x = 1, x = -1 ja ratkaisemalla saatu lineaarinen yhtälöryhmä
3x2 = 0
arvot x = 0, x = 1, x = -1 ja ratkaisemalla saatu lineaarinen yhtälöryhmä
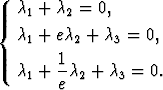
Saatu yleinen ratkaisu on kaikkialla säännöllinen. Differentiaaliyhtälö ei kuitenkaan täytä alkuarvoprobleeman ratkaisun olemassaoloa koskevan lauseen ehtoja. Normaalimuodossa differentiaaliyhtälö nimittäin on
y''' - 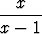 y'' +
y'' + 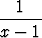 y' = 0,
y' = 0,
joten vaatimukset kerroinfunktioiden jatkuvuudesta eivät täyty välillä, joka sisältää pisteen x = 1. Ratkaisujen kannalta ei tämä piste kuitenkaan näytä poikkeukselliselta ainakaan ensi näkemältä. Se on kuitenkin piste, jossa yhtälön ratkaisu ei toteuta mitä tahansa alkuehtoa. Yleisen ratkaisun derivaatat nimittäin ovat
y' = C2ex + 2C3x ja y'' = C2ex + 2C3,
ja pisteessä x = 1 nämä saavat saman arvon vakioista C2 ja C3 riippumatta. Ratkaisua ei siis löydy, jos alkuehdossa vaaditaan, että y'(1) ja y''(1) saavat eri suuret arvot.