Vakiokertoimisen lineaariyhtälön karakteristisen yhtälön useampikertaiset juuret

Kiinnitetään aluksi kolme vakiota.

Tarkastelun kohteena olkoon kertalukua n oleva vakiokertoiminen homogeeninen differentiaaliyhtälö:

> n:= 3;

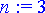
Tämän karakteristinen polynomi on myös astetta n . Polynomilla olkoon nollakohta r , jonka kertaluku on p (<= n ):

> p:= 2;

Tarkoituksena on tutkia, onko 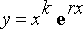yhtälön ratkaisu, kun k = 0, 1, 2, ..., q (luontevimmin q >= p ):

> q:= 3;

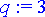
Vakiokertoimisten yhtälöiden teorian mukaan näin pitäisi olla arvoon k = p - 1 saakka.

Differentiaaliyhtälö on

> diffyht:= sum(a[k]*diff(y(x), [x$k]), k=0..n)=0;

Karakteristinen yhtälö saadaan sijoittamalla yhtälöön yrite 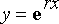ja jakamalla sijoittamisen jälkeen eksponenttitekijä pois. Samaan tulokseen päästään korvaamalla differentiaaliyhtälössä derivaatat vastaavilla muuttujan r potensseilla:

> seq(diff(y(x), [x$k])=r^k, k=0..n):
karaktyht:= subs({%}, diffyht);

Luku r on p -kertainen juuri, jos ja vain jos se on myös derivaattojen nollakohta kertalukuun p - 1 saakka. Kertaluku voidaan siten karakterisoida seuraavilla ehdoilla:

> ehdot:= seq(diff(karaktyht, [r$k]), k=0..p-1);

Sijoitetaan ratkaisut 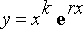(0 <= k <= q ) differentiaaliyhtälöön ja tutkitaan, toteutuuko tämä, kun r täyttää edellä asetetut ehdot:

> subs(y(x)=x^k*exp(r*x), diffyht):
sij:= seq(%, k=0..q):
simplify({%});

> simplify({sij}, {ehdot});

Yhtälön toteuttavia ratkaisuja näyttää todellakin olevan nollakohdan r kertaluvun p mukainen määrä, kuten teorian mukaan pitääkin.

Polynomiehtojen käsittelyyn symboliset laskentajärjestelmät kuten Maple käyttävät ns. Gröbnerin kantoja . Probleeman monimutkaistuessa näiden käyttö tulee kuitenkin raskaaksi hyvin nopeasti. Vaikka edellä oleva lasku voidankin periaatteessa laskea millä tahansa arvoilla n , p , q laskenta alkaa arvojen kasvaessa vaatia aikaa ja muistia todella paljon. Lukija kokeilkoon!