![x[0]](Images/nummen1.gif) ) =
) =
![y[0]](Images/nummen2.gif) , ratkaisemiseksi voidaan ohjelmoida
Maple
lle
eulernum
-nimiseksi proseduuriksi seuraavalla tavalla (solu on ajettava, jotta määritelmä tulee voimaan):
, ratkaisemiseksi voidaan ohjelmoida
Maple
lle
eulernum
-nimiseksi proseduuriksi seuraavalla tavalla (solu on ajettava, jotta määritelmä tulee voimaan): | nummen.mws |
Eulerin menetelmä alkuarvoprobleeman
y
' = f(
x
,
y
), y(
![x[0]](Images/nummen1.gif) ) =
) =
![y[0]](Images/nummen2.gif) , ratkaisemiseksi voidaan ohjelmoida
Maple
lle
eulernum
-nimiseksi proseduuriksi seuraavalla tavalla (solu on ajettava, jotta määritelmä tulee voimaan):
, ratkaisemiseksi voidaan ohjelmoida
Maple
lle
eulernum
-nimiseksi proseduuriksi seuraavalla tavalla (solu on ajettava, jotta määritelmä tulee voimaan):
>
eulernum:=proc(f, x0, y0, h, xend)
local kend, x, y, i;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to kend do
x[i]:= x[i-1]+h;
y[i]:= y[i-1]+h*f(x[i-1], y[i-1]);
od;
return [seq([x[k], y[k]], k=0..kend)];
end:
Proseduurin ensimmäinen argumentti on differentiaaliyhtälön oikean puolen funktio f Maple n funktioksi määriteltynä, kaksi seuraavaa määrittävät alkuehdon, neljäs on askelpituus. Laskenta tapahtuu välillä [x0,xend] .
Proseduurin toisella rivillä lasketaan tarvittavien askelten lukumäärä
kend
. Kolmannella ja neljännellä rivillä määritellään alkuarvot.
For
-silmukassa lasketaan numeerisen ratkaisun hilapisteet Eulerin menetelmällä. Viimeisellä rivillä palautetaan vastaus listana koottuna
xy
-pareiksi.
Numeerinen ratkaiseminen tapahtuu antamalla tarvittavat argumentit eulernum -funktiolle, jolloin tulokseksi saadaan lista hilapisteiden koordinaateista. Argumentit voidaan tallettaa muillekin nimille kuin funktion määrittelyssä käytetyille tai antaa myös suoraan numeroina (esimerkiksi askel:= 0.1 , eulernum(f,x0,y0,askel,xend) tai eulernum(unapply(2*x*y,x,y),0,1,0.1,2) .
> f:= unapply(2*x*y, x, y);
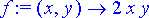
> h:= 0.1;
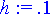
> x0:= 0;
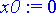
> y0:= 1;
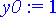
> xend:= 2;
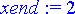
> eulerdata:= eulernum(f, x0, y0, h, xend);
![eulerdata := [[0, 1], [.1, 1.], [.2, 1.02], [.3, 1....](Images/nummen8.gif)
![eulerdata := [[0, 1], [.1, 1.], [.2, 1.02], [.3, 1....](Images/nummen9.gif)
![eulerdata := [[0, 1], [.1, 1.], [.2, 1.02], [.3, 1....](Images/nummen10.gif)
![eulerdata := [[0, 1], [.1, 1.], [.2, 1.02], [.3, 1....](Images/nummen11.gif)
![eulerdata := [[0, 1], [.1, 1.], [.2, 1.02], [.3, 1....](Images/nummen12.gif)
Datan perusteella voidaan piirtää kuva ratkaisua approksimoivista pisteistä.
>
eulerkuva:= plot(eulerdata, style=point):
eulerkuva;
![[Maple Plot]](Images/nummen13.gif)
Samaan tapaan voidaan ohjelmoida parannettu Eulerin menetelmä, Rungen – Kuttan menetelmä ja Adamsin – Bashforthin menetelmä:
>
pareuler:= proc(f, x0, y0, h, xend)
local kend, x, y, i;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to kend do
x[i]:= x[i-1]+h;
y[i]:= y[i-1]+
h/2*(f(x[i-1], y[i-1])+
f(x[i], y[i-1]+h*f(x[i-1], y[i-1])));
od;
return [seq([x[k],y[k]], k=0..kend)];
end:
>
rungekutta:= proc(f, x0, y0, h, xend)
local kend, x, y, i, k1, k2, k3, k4;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to kend do
x[i]:= x[i-1]+h;
k1:= h*f(x[i-1], y[i-1]);
k2:= h*f(x[i-1]+h/2, y[i-1]+k1/2);
k3:= h*f(x[i-1]+h/2, y[i-1]+k2/2);
k4:= h*f(x[i-1]+h, y[i-1]+k3);
y[i]:= y[i-1]+1/6*(k1+2*k2+2*k3+k4);
od;
return [seq([x[k], y[k]], k=0..kend)];
end:
>
adamsbashforth:= proc(f, x0, y0, h, xend)
local kend, x, y, i, k1, k2, k3, k4;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to 3 do
x[i]:= x[i-1]+h;
k1:= h*f(x[i-1], y[i-1]);
k2:= h*f(x[i-1]+h/2, y[i-1]+k1/2);
k3:= h*f(x[i-1]+h/2, y[i-1]+k2/2);
k4:= h*f(x[i-1]+h, y[i-1]+k3);
y[i]:= y[i-1]+1/6*(k1+2*k2+2*k3+k4);
od;
for i from 4 to kend do
x[i]:= x[i-1]+h;
y[i]:= y[i-1]+h/24*(
55*f(x[i-1], y[i-1])-
59*f(x[i-2], y[i-2])+
37*f(x[i-3], y[i-3])-
9*f(x[i-4], y[i-4]))
od;
return [seq([x[k], y[k]], k=0..kend)];
end:
Näiden avulla muodostetut ratkaisut ja vastaavat kuvat:
> pareulerdata:= pareuler(f, x0, y0, h, xend);
![pareulerdata := [[0, 1], [.1, 1.010000000], [.2, 1....](Images/nummen14.gif)
![pareulerdata := [[0, 1], [.1, 1.010000000], [.2, 1....](Images/nummen15.gif)
![pareulerdata := [[0, 1], [.1, 1.010000000], [.2, 1....](Images/nummen16.gif)
![pareulerdata := [[0, 1], [.1, 1.010000000], [.2, 1....](Images/nummen17.gif)
![pareulerdata := [[0, 1], [.1, 1.010000000], [.2, 1....](Images/nummen18.gif)
![pareulerdata := [[0, 1], [.1, 1.010000000], [.2, 1....](Images/nummen19.gif)
>
pareulerkuva:= plot(pareulerdata, style=point):
pareulerkuva;
![[Maple Plot]](Images/nummen20.gif)
> rungekuttadata:= rungekutta(f, x0, y0, h, xend);
![rungekuttadata := [[0, 1], [.1, 1.010050166], [.2, ...](Images/nummen21.gif)
![rungekuttadata := [[0, 1], [.1, 1.010050166], [.2, ...](Images/nummen22.gif)
![rungekuttadata := [[0, 1], [.1, 1.010050166], [.2, ...](Images/nummen23.gif)
![rungekuttadata := [[0, 1], [.1, 1.010050166], [.2, ...](Images/nummen24.gif)
![rungekuttadata := [[0, 1], [.1, 1.010050166], [.2, ...](Images/nummen25.gif)
![rungekuttadata := [[0, 1], [.1, 1.010050166], [.2, ...](Images/nummen26.gif)
>
rungekuttakuva:= plot(rungekuttadata, style=point):
rungekuttakuva;
![[Maple Plot]](Images/nummen27.gif)
> adamsbashforthdata:= adamsbashforth(f, x0, y0, h,xend);
![adamsbashforthdata := [[0, 1], [.1, 1.010050166], [...](Images/nummen28.gif)
![adamsbashforthdata := [[0, 1], [.1, 1.010050166], [...](Images/nummen29.gif)
![adamsbashforthdata := [[0, 1], [.1, 1.010050166], [...](Images/nummen30.gif)
![adamsbashforthdata := [[0, 1], [.1, 1.010050166], [...](Images/nummen31.gif)
![adamsbashforthdata := [[0, 1], [.1, 1.010050166], [...](Images/nummen32.gif)
![adamsbashforthdata := [[0, 1], [.1, 1.010050166], [...](Images/nummen33.gif)
>
adamsbashforthkuva:= plot(adamsbashforthdata, style=point):
adamsbashforthkuva;
![[Maple Plot]](Images/nummen34.gif)
Esimerkkinä oleva alkuarvoprobleema on myös ratkaistavissa algebrallisesti, jolloin voidaan verrata eri menetelmien tarkkuutta toisiinsa ja myös tarkkaan ratkaisuun:
> tarkkaratkaisu:= dsolve({diff(y(x), x)=2*x*y(x), y(x0)=y0}, y(x));
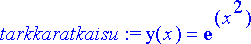
>
tarkkakuva:= plot(rhs(tarkkaratkaisu), x=0..xend):
tarkkakuva;
![[Maple Plot]](Images/nummen36.gif)
Kaikki ratkaisut samassa kuvassa:
> with(plots):
Warning, the name changecoords has been redefined
> display(eulerkuva, pareulerkuva, rungekuttakuva, adamsbashforthkuva, tarkkakuva);
![[Maple Plot]](Images/nummen37.gif)
Lopuksi eri menetelmillä saadut arvot tarkasteluvälin loppupisteessä:
>
eulerdata[-1][2],
pareulerdata[-1][2],
rungekuttadata[-1][2],
adamsbashforthdata[-1][2],
evalf(subs(x=2,rhs(tarkkaratkaisu)));
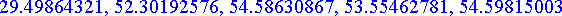
Edellä olevia syötteitä voi muuntaa ja tämän jälkeen ajaa koko muistikirjan yhdellä kerralla (valikko
Edit
/
Execute
/
Worksheet
).