 ,
,
| varaht2.mws |
Jousen puristumista ja venymistä voidaan kuvata varsin yksinkertaisella matemaattisella mallilla
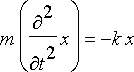 ,
,
missä x on jousen poikkeama tasapainoasemasta ja k jouselle tyypillinen jousivakio.
Tässä esimerkissä tarkastelun kohteena on oheisen kuvion mukainen jousisysteemi, jossa kolme kappaletta massoiltaan
![m[1]](Images/varaht22.gif) ,
,
![m[2]](Images/varaht23.gif) ja
ja
![m[3]](Images/varaht24.gif) on liitetty toisiinsa ja kiinnikkeeseen neljällä jousella jousivakioiltaan
on liitetty toisiinsa ja kiinnikkeeseen neljällä jousella jousivakioiltaan
![k[1]](Images/varaht25.gif) ,
,
![k[2]](Images/varaht26.gif) ,
,
![k[3]](Images/varaht27.gif) ja
ja
![k[4]](Images/varaht28.gif) . Kappaleet voivat liikkua vain pystysuorassa suunnassa.
. Kappaleet voivat liikkua vain pystysuorassa suunnassa.
![[Maple Bitmap]](Images/varaht29.gif)
Kappaleiden paikkakoordinaatit
![x[1]](Images/varaht210.gif) ,
,
![x[2]](Images/varaht211.gif) ja
ja
![x[3]](Images/varaht212.gif) ilmoitetaan poikkeamina lepotilasta, ylöspäin positiivisena ja alaspäin negatiivisena. Newtonin lain mukaan kuhunkin kappaleeseen vaikuttava voima on toisaalta kappaleen massa kerrottuna sen kiihtyvyydellä eli paikkakoordinaatin toisella aikaderivaatalla, toisaalta kyseessä on jousien aiheuttama harmoninen voima. Systeemin liikeyhtälöt ovat siten toisen kertaluvun differentiaaliyhtälöitä, yksi yhtälö jokaista kappaletta kohden.
ilmoitetaan poikkeamina lepotilasta, ylöspäin positiivisena ja alaspäin negatiivisena. Newtonin lain mukaan kuhunkin kappaleeseen vaikuttava voima on toisaalta kappaleen massa kerrottuna sen kiihtyvyydellä eli paikkakoordinaatin toisella aikaderivaatalla, toisaalta kyseessä on jousien aiheuttama harmoninen voima. Systeemin liikeyhtälöt ovat siten toisen kertaluvun differentiaaliyhtälöitä, yksi yhtälö jokaista kappaletta kohden.
![m[1]*diff(x[1],`$`(t,2)) = -k[1]*x[1]+k[2]*(x[2]-x[...](Images/varaht213.gif) ,
,
![m[2]*diff(x[2],`$`(t,2)) = -k[2]*(x[2]-x[1])-k[4]*(...](Images/varaht214.gif) ,
,
![m[3]*diff(x[3],`$`(t,2)) = -k[3]*(x[3]-x[1])+k[4]*(...](Images/varaht215.gif) .
.
Tutkitaan jousisysteemin käyttäytymistä ratkaisemalla differentiaaliyhtälöryhmä
Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.
> restart;
Asetetaan kappaleiden massoille ja jousivakioille numeeriset arvot:
> m[1]:= 2: m[2]:= 1: m[3]:= 1: k[1]:= 4: k[2]:= 2: k[3]:= 2: k[4]:= 1:
Muodostetaan systeemin differentiaaliyhtälöryhmä.
> ryhma:= m[1]*diff(x[1](t), t$2)=-k[1]*x[1](t)+k[2]*(x[2](t)-x[1](t))+k[3]*(x[3](t)-x[1](t)), m[2]*diff(x[2](t), t$2)=-k[2]*(x[2](t)-x[1](t))-k[4]*(x[2](t)-x[3](t)), m[3]*diff(x[3](t), t$2)=-k[3]*(x[3](t)-x[1](t))+k[4]*(x[2](t)-x[3](t));
,`$`(t,2)) = -8*x[1](t)+2*x[...](Images/varaht216.gif)
,`$`(t,2)) = -8*x[1](t)+2*x[...](Images/varaht217.gif)
Kerätään kappaleiden sijaintia osoittavat funktiot listaksi, samoin näiden derivaatat.
> funktiot:= x[1](t), x[2](t), x[3](t);
, x[2](t), x[3](t)](Images/varaht218.gif)
> derivaatat:= [D(x[1])(t), D(x[2])(t), D(x[3])(t)];
![derivaatat := [D(x[1])(t), D(x[2])(t), D(x[3])(t)]](Images/varaht219.gif)
Systeemiä tarkastellaan siten, että se sysätään hetkellä t = 0 liikkeelle lepotilasta antamalla kullekin kappaleelle jokin alkunopeus. Alkuehdossa annetaan siten paikkakoordinaateille arvo 0 ja nopeuksille eli paikkakoordinaattien derivaatoille jotkin haluttua liiketilaa vastaavat arvot:
> alkusijainti:= x[1](0)=0, x[2](0)=0, x[3](0)=0;
 = 0, x[2](0) = 0, x[3](0) =...](Images/varaht220.gif)
> alkunopeus:= [D(x[1])(0)=-10, D(x[2])(0)=10, D(x[3])(0)=30];
![alkunopeus := [D(x[1])(0) = -10, D(x[2])(0) = 10, D...](Images/varaht221.gif)
Saatu differentiaaliyhtälöryhmä ratkaistaan Maple n dsolve -komennolla ja sievennetään.
>
liike:= dsolve({ryhma, alkusijainti, alkunopeus[]}, {funktiot}):
simplify(%);
 = 5*sin(2*t)+5/2*sin(1/2*t*sqrt(2)*sqrt(5)...](Images/varaht222.gif)
 = 5*sin(2*t)+5/2*sin(1/2*t*sqrt(2)*sqrt(5)...](Images/varaht223.gif)
 = 5*sin(2*t)+5/2*sin(1/2*t*sqrt(2)*sqrt(5)...](Images/varaht224.gif)
 = 5*sin(2*t)+5/2*sin(1/2*t*sqrt(2)*sqrt(5)...](Images/varaht225.gif)
 = 5*sin(2*t)+5/2*sin(1/2*t*sqrt(2)*sqrt(5)...](Images/varaht226.gif)
 = 5*sin(2*t)+5/2*sin(1/2*t*sqrt(2)*sqrt(5)...](Images/varaht227.gif)
Tuloksesta nähdään, että systeemin liiketila muodostuu kolmesta erilaisesta värähtelystä. Näiden taajuudet ilmenevät lausekkeissa esiintyvistä sinifunktioista,
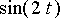 ,
,
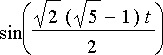 ,
,
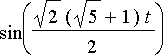 .
.
Seuraava koodi määrittelee kappaleen liikkeessä tarvittavat työkalut. Kysessä on Maple lla kirjoitettu ohjelmakoodi.
> with(plots): with(plottools):
Warning, the name changecoords has been redefined
>
jousi:= proc(hor, ala, yla, paa, jaksot)
local ampl, jakso;
ampl:= 3;
jakso:= (yla-ala-2*paa)/jaksot;
plot([[hor+ampl*sin(2*Pi*r/jakso),
r+ala+paa, r=0..jaksot*jakso],
[hor, ala+r, r=0..paa],
[hor, yla-r, r=0..paa]], color=black);
end:
kappale:= proc(hor, ver, lev, kor, teksti)
display(rectangle([hor-0.5*lev,
ver+0.5*kor], [hor+0.5*lev,
ver-0.5*kor], color=gray),
textplot([35, ver, teksti])
);
end:
jousisyst:= proc(y0, t0)
local lev, kor, paa, lepo1, lepo2,
lepo3, y1, y2, y3;
lev:= 20; kor:= 10; paa:= 5; lepo1:= 50;
lepo2:= 150; lepo3:= 100;
y1:= -lepo1+subs(t=t0/(2*Pi),
subs(y0, x[1](t)));
y2:= -lepo2+subs(t=t0/(2*Pi),
subs(y0,x[2](t)));
y3:= -lepo3+subs(t=t0/(2*Pi),
subs(y0,x[3](t)));
display(rectangle([-50,0], [50,5],
color=gray),
kappale(0, y1, lev, kor, 'm1'),
kappale(0, y2, lev, kor, 'm2'),
kappale(lev/2, y3, lev, kor, 'm3'),
jousi(0, y1+kor/2, 0, 5, 5),
jousi(-lev/2, y2+kor/2,
y1-kor/2, 5,10),
jousi(lev/2, y3+kor/2,
y1-kor/2, 5, 5),
jousi(lev/2, y2+kor/2,
y3-kor/2, 5, 5)
);
end:
Animaatio on lista peräkkäisiä kuvia, jotka on ensin laskettava. Animaatio käynnistyy viemällä hiiren osoitin kuvan päälle ja valitsemalla hiiren oikealla napilla esiin tulevasta valikosta A n imation -> P l ay . Animaatiosta saa jatkuvan valitsemalla em. valikosta A n imation -> C ontinuous .
> display(seq(jousisyst(liike, u), u=0..29), insequence=true, axes=NONE, scaling=CONSTRAINED);
Kiinnostava tilanne syntyy, jos systeemin liikkeessä esiintyy vain yksi edellä mainituista kolmesta taajuudesta. Tällaiseen on mahdollista päästä valitsemalla alkunopeudet sopivasti. Seuraava lista sisältää kutakin taajuutta vastaavat alkunopeuksien suhteet. Seuraavat kolme komentoa asettavat alkunopeusasetukseksi kunkin näistä vuorollaan. Lukija tutkikoon, millaisia systeemin liikkeitä tällöin syntyy!
> moodit:=[0, -1, 1], [1/2*(-1-sqrt(5)), 1, 1], [1/2*(-1+sqrt(5)), 1, 1];
![moodit := [0, -1, 1], [-1/2-1/2*sqrt(5), 1, 1], [-1...](Images/varaht232.gif)
> alkunopeus:= zip((x, y)->x=y, subs(t=0, derivaatat), 15*moodit[1]);
![alkunopeus := [D(x[1])(0) = 0, D(x[2])(0) = -15, D(...](Images/varaht233.gif)
> alkunopeus:= zip((x, y)->x=y, subs(t=0, derivaatat), 15*moodit[2]);
![alkunopeus := [D(x[1])(0) = -15/2-15/2*sqrt(5), D(x...](Images/varaht234.gif)
> alkunopeus:= zip((x, y)->x=y, subs(t=0, derivaatat), 15*moodit[3]);
![alkunopeus := [D(x[1])(0) = -15/2+15/2*sqrt(5), D(x...](Images/varaht235.gif)