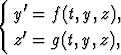
Paitsi ensimmäisen myös toisen kertaluvun differentiaaliyhtälöistä saadaan melkoisesti tietoa graafisilla tarkasteluilla ilman, että yhtälöä ratkaistaan. Tällöin yhtälö usein kirjoitetaan ensimmäistä kertalukua olevan normaaliryhmän muotoon. Seuraavassa tarkasteltava differentiaaliyhtälöryhmä voi olla tällainen normaaliryhmä tai mikä tahansa ensimmäisen kertaluvun differentiaaliyhtälöryhmä.
Normaalimuodossa oleva ensimmäisen kertaluvun differentiaaliyhtälöryhmä on
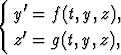
missä riippumattomana muuttujana on t ja tuntemattomina funktioina y(t) ja z(t).
Yhtälöryhmän ratkaisut ovat funktiopareja (y(t), z(t)), ja ne voidaan mieltää yz-tason käyriksi riippumattoman muuttujan t ollessa käyräparametrin asemassa. Tällaista ratkaisukäyrien esitystä yz-tasossa kutsutaan faasitasoesitykseksi.
Ratkaisukäyrän tangenttivektori on (y'(t), z'(t)), ja sen laskemiseen voidaan käyttää alkuperäistä differentiaaliyhtälöryhmää: Jos yhtälöryhmä on autonominen, ei oikea puoli riipu eksplisiittisesti muuttujasta t, jolloin
(y'(t), z'(t)) = (f(y, z), g(y, z)).
Pisteeseen (y, z) liittyvä tangenttisuunta saadaan siis lasketuksi. Tällä tavoin voidaan muodostaa faasitasoratkaisuille suuntakenttä ja sen perusteella hahmotella ratkaisukäyrät.
Edellä sanottu antaa myös kvalitatiivisen tuloksen: Jos pisteessä (y, z) ainakin toinen
luvuista f(y, z) ja g(y, z) on 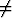 0, on tangenttisuunta tässä pisteessä yksikäsitteinen.
Tällöin kaksi eri ratkaisukäyrää eivät voi leikata toisiaan. Poikkeuksellisia pisteitä ovat ne,
joissa f(y, z) = g(y, z) = 0, jolloin tangenttisuunta jää epämääräiseksi.
0, on tangenttisuunta tässä pisteessä yksikäsitteinen.
Tällöin kaksi eri ratkaisukäyrää eivät voi leikata toisiaan. Poikkeuksellisia pisteitä ovat ne,
joissa f(y, z) = g(y, z) = 0, jolloin tangenttisuunta jää epämääräiseksi.
Jos yhtälöryhmä ei ole autonominen, riippuu tangenttisuunta paitsi faasitason pisteen koordinaateista (y, z) myös muuttujasta t. Tällöinkin voidaan muodostaa suuntakenttiä, mutta ne ovat erilaisia muuttujan t eri arvoilla. Niistä ei voida päätellä ratkaisukäyrän kulkua, koska tietyyn pisteeseen (y, z) kuuluvaa parametriarvoa t ei tunneta.
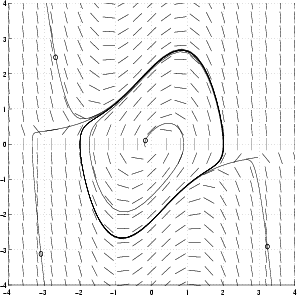
Oheinen kuvio on autonomisen van der Polin yhtälön y'' - 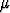 (1 - y2)y' + y = 0
ratkaisukäyrien faasitasoesitys, kun
(1 - y2)y' + y = 0
ratkaisukäyrien faasitasoesitys, kun 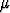 = 1. Vastaava normaaliryhmä on
= 1. Vastaava normaaliryhmä on
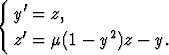
Sovelluksissa riippumaton muuttuja on usein aika ja sen symbolina on t. Tuntemattomat funktiot y(t) ja z(t) kuvaavat tarkasteltavan systeemin tilaa hetkellä t. Kyseessä voi esimerkiksi olla partikkelin paikka ja nopeus, jolloin z = y'.