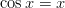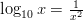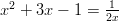Yhtälöt
Yksinkertaisimmassa yhtälötyypissä on yksi tuntematon, jota yleensä merkitään x:llä. Tuntemattomia voi kuitenkin olla useampiakin. Tällöin usein myös yhtälöitä on useampia ja kyseessä on yhtälöryhmä.
Yhtälön tai yhtälöryhmän ratkaisemisessa yhtälöä tai ryhmää muunnetaan siten, että se säilyy yhtäpitävänä alkuperäisen kanssa. Tämä tapahtuu yleensä kohdistamalla sama operaatio tai funktio yhtäläisyysmerkin eri puolilla oleviin lausekkeisiin tavoitteena saada tuntematon jäämään yksinään toiselle puolelle yhtäläisyysmerkkiä.
Jos tässä onnistutaan, niin tuloksena saadaan algebrallinen ratkaisu. Aina ei ratkaiseminen tällä tavoin onnistu, vaan joudutaan turvautumaan johonkin numeeriseen menettelyyn, jolla saadaan ratkaisun approksimaatio yleensä niin monen numeron tarkkuudella kuin halutaan. Tunnetuin numeerinen menetelmä on Newtonin iteraatio.
Kuvaajien piirtäminen auttaa usein hahmottamaan tilannetta ja selvittämään juurien lukumäärää ja sijaintia.
Yhtälöt voidaan jaotella sen mukaan, minkälaisia tuntemattoman sisältäviä lausekkeita niissä on. Täten puhutaan polynomiyhtälöistä, juuriyhtälöistä, itseisarvoyhtälöistä jne.
Transkendenttiyhtälöt sisältävät muitakin tuntemattoman funktioita kuin potensseja. Niiden ratkaiseminen perustuu esiintyvien funktioiden ominaisuuksiin.
Esimerkkejä
- Erilaisia yhtälöitä:
Itseisarvoyhtälö: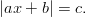
Neljännen asteen polynomiyhtälö: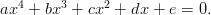
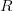 -säteisen pallon, jonka keskipiste on
-säteisen pallon, jonka keskipiste on 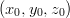 , yhtälö:
, yhtälö: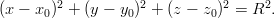
Eräs trigonometrinen yhtälö: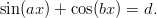
- Yhtälöä
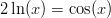 ei osata ratkaista algebrallisesti.
ei osata ratkaista algebrallisesti.
Ainakin yksi ratkaisu on olemassa. Kosini on jatkuva ja aidosti laskeva funktio välillä![[0,π ]](yhtalo7x.gif) ja luonnollinen logaritmi jatkuva ja aidosti kasvava
puoliavoimella välillä
ja luonnollinen logaritmi jatkuva ja aidosti kasvava
puoliavoimella välillä ![]0,π ]](yhtalo8x.gif) . Tarkastellaan yhtälön kummankin
puolen arvoja välin päätepisteissä:
. Tarkastellaan yhtälön kummankin
puolen arvoja välin päätepisteissä:
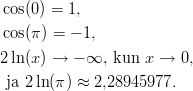
Arvoista voi päätellä, että yhtälöllä on ainakin yksi ratkaisu. Hyvän approksimaation voi löytää numeerisella menetelmällä, esimerkiksi Newtonin menetelmällä.
- Joihinkin yhtälöihin on olemassa suoria ratkaisukaavoja, esimerkiksi
toisen asteen polynomiyhtälöön
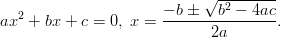
Kaikki ratkaisukaavat eivät kuitenkaan ole kovin käteviä käytössä, hyvänä esimerkkinä 3. asteen polynomiyhtälön ratkaisukaava.
3. asteen yhtälön ratkaisukaava
- Tutkitaan transkendenttiyhtälön
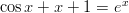 ratkaisuja
piirtämällä kuvaajat.
ratkaisuja
piirtämällä kuvaajat.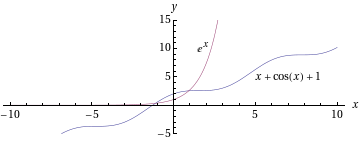
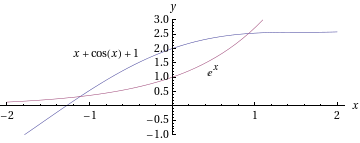
Kuvaajista näemme, että yhtälöllä on kaksi ratkaisua ja ne ovat noin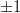 . Tarkemmat likiarvot voidaan hakea esimerkiksi
haarukoimalla funktiota
. Tarkemmat likiarvot voidaan hakea esimerkiksi
haarukoimalla funktiota 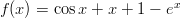 , kunnes saadaan
vastaus riittävällä tarkkuudella:
, kunnes saadaan
vastaus riittävällä tarkkuudella:
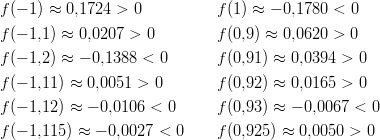
Yhtälön ratkaisut kahden desimaalin tarkkuudella ovat:
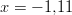 ja
ja 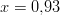 .
.

Harjoitustehtäviä
-
- Toteuttaako
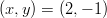 yhtälön
yhtälön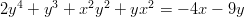 ?
?
- Toteuttaako
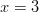 yhtälön
yhtälön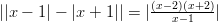 ?
?
- Toteuttaako
- Piirrä yhtälön molemmat puolet ja arvioi eräs ratkaisu.
-
Tehtävien vastaukset: