Sykliset ryhmät

Määritelmä. Ryhmää (G,*) sanotaan sykliseksi, jos G on yhden alkion generoima, eli jos on olemassa sellainen a G, että < a > = G.

Lause. Olkoon (G,*) syklinen ryhmä, siis on olemassa sellainen a G, että G = < a > . Olkoon e ryhmän neutraalialkio.

Jos (G,*) on äärellinen ryhmä, niin

missä positiivinen luku n on pienin sellainen eksponentti, että aⁿ = e.

Jos (G,*) on ääretön ryhmä, niin

ja kaikki potenssit a^m (m ) ovat erisuuria, erityisesti a^me kaikilla kokonaisluvuilla m0.

Todistus. Ryhmän generointi -sivun lauseen perusteella on G = {a^m | m }.

Oletetaan ensin, että (G,*) on äärellinen. Silloin kaikki potenssit a⁰,a,a²,a³,a⁴,... eivät voi olla erisuuria, vaan on olemassa sellaiset luvut l ja k, että a^l = a^k ja l > k. Koska a^k * (a^l-k) = a^l = a^k = a^k * e niin ryhmän yhtälön supistussäännön nojalla a^l-k = e. Koska l - k > 0, on olemassa sellaisia positiivisia kokonaislukuja j, joilla a^j = e. Olkoon n pienin näistä.

Jakoalgoritmin mukaan jokainen eksponentti m voidaan kirjoittaa muodossa m = qn + r, missä 0 < r < n - 1. Nyt

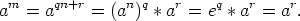
Siis kaikki joukon G alkiot ovat muotoa a^r, missä 0 < r < n - 1, siis G = {a⁰,a,...,a^n-1}. Kaikki tämän joukon alkiot ovat erisuuria, sillä toistamalla aikaisempi päättely joukon G alkioille löydettäisiin jokin luku t, jolle a^t = e ja 0 < t < n - 1. Tämä on kuitenkin ristiriidassa luvun n minimaalisuuden kanssa. Siis joukko G on väitettyä muotoa.

Jos G on ääretön ovat kaikki potenssit a^m, missä m , erisuuria, sillä muuten päädyttäisiin äärelliseen ryhmään kuten edellä.

Ryhmän kertaluku on määritelmän mukaan ryhmän alkioiden lukumäärä. Määritellään seuraavassa ryhmän alkion kertaluku.

Määritelmä. Olkoon (G,*) ryhmä ja a G. Alkion a generoiman aliryhmän (< a >,*) kertalukua sanotaan alkion a kertaluvuksi. Alkion a kertaluvusta käytetään merkintää ord(a), siis

Edellisestä lauseesta seuraa, että alkio a on (äärellistä) kertalukua n jos ja vain jos n on pienin sellainen eksponentti, jolla aⁿ = e. Tällöin lisäksi alkion a potenssit a⁰ = e,a,a²,...,a^n-1 ovat kaikki erisuuria. Huomaa, että ord(a) = 1 jos ja vain jos a = e.

Linkit:
Huomioita ryhmästä
Jakoalgoritmi
Ryhmän generointi
Ryhmän perusominaisuuksia