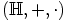 ,
, 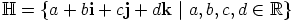 , ns. kvaternionirengas,
jonka nolla- ja ykkösalkiot ovat
, ns. kvaternionirengas,
jonka nolla- ja ykkösalkiot ovat 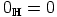 ja
ja 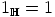 , jonka operaatiot
, jonka operaatiot 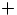 ja
ja  rajoitettuna reaaliluvuille
rajoitettuna reaaliluvuille 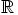 ovat reaalilukujen tavanomaiset yhteen- ja
kertolaskut ja jossa pätee laskusäännöt:
ovat reaalilukujen tavanomaiset yhteen- ja
kertolaskut ja jossa pätee laskusäännöt:
Olkoon 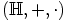 ,
, 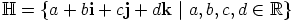 , ns. kvaternionirengas,
jonka nolla- ja ykkösalkiot ovat
, ns. kvaternionirengas,
jonka nolla- ja ykkösalkiot ovat 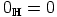 ja
ja 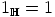 , jonka operaatiot
, jonka operaatiot 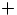 ja
ja  rajoitettuna reaaliluvuille
rajoitettuna reaaliluvuille 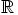 ovat reaalilukujen tavanomaiset yhteen- ja
kertolaskut ja jossa pätee laskusäännöt:
ovat reaalilukujen tavanomaiset yhteen- ja
kertolaskut ja jossa pätee laskusäännöt:
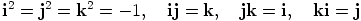 |
ja
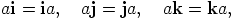 |
aina kun 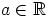 .
.
a) Laske 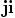 ,
, 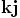 ja
ja 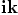 .
.
b) Olkoon kvaternionin 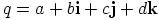 konjugaattikvaternioni alkio
konjugaattikvaternioni alkio
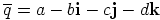 . Laske
. Laske 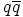 .
.
c) Osoita, että renkaan 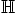 yksikköryhmä on
yksikköryhmä on 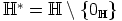 .
.
d) Merkitään 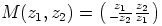 , kaikilla
, kaikilla 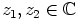 . Osoita, että
joukko
. Osoita, että
joukko
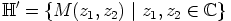 |
muodostaa renkaan 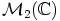 alirenkaan.
alirenkaan.
e) Osoita, että renkaat 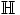 ja
ja 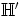 ovat isomorfiset.
ovat isomorfiset.