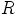 joukko,
joukko, 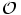 joukko siinä määriteltyjä binäärioperaatioita (paria
joukko siinä määriteltyjä binäärioperaatioita (paria
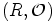 kutsutaan algebraksi, rengas on siis eräs erikoistapaus algebrasta) ja
kutsutaan algebraksi, rengas on siis eräs erikoistapaus algebrasta) ja 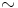 ekvivalenssirelaatio joukossa
ekvivalenssirelaatio joukossa 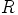 . Relaatiota
. Relaatiota 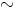 sanotaan kongruenssiksi, jos se
täyttää ehdon
sanotaan kongruenssiksi, jos se
täyttää ehdon
Olkoon 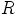 joukko,
joukko, 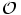 joukko siinä määriteltyjä binäärioperaatioita (paria
joukko siinä määriteltyjä binäärioperaatioita (paria
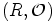 kutsutaan algebraksi, rengas on siis eräs erikoistapaus algebrasta) ja
kutsutaan algebraksi, rengas on siis eräs erikoistapaus algebrasta) ja 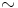 ekvivalenssirelaatio joukossa
ekvivalenssirelaatio joukossa 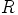 . Relaatiota
. Relaatiota 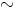 sanotaan kongruenssiksi, jos se
täyttää ehdon
sanotaan kongruenssiksi, jos se
täyttää ehdon
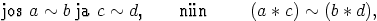 |
kaikilla joukon 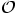 operaatioilla
operaatioilla 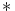 ja joukon
ja joukon 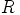 alkioilla
alkioilla 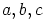 ja
ja 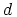 (vertaa
lukukongruenssiin).
(vertaa
lukukongruenssiin).
a) Osoita, että ehdolla
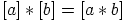 |
määritelty joukon 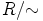 binäärioperaatio on hyvin määritelty eli ehdoista
binäärioperaatio on hyvin määritelty eli ehdoista
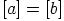 ja
ja 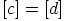 seuraa
seuraa 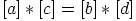 , jos
, jos 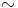 on kongruenssi. (Tämä
merkitsee, että
on kongruenssi. (Tämä
merkitsee, että 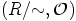 on algebra, jos
on algebra, jos 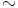 on kongruenssi.)
on kongruenssi.)
b) Olkoon nyt 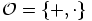 ja
ja 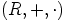 (kommutatiivinen) rengas. Osoita, että
myös
(kommutatiivinen) rengas. Osoita, että
myös 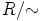 on (kommutatiivinen) rengas, ts. kaikki (kommutatiivisen) renkaan
ehdot periytyvät renkaalta
on (kommutatiivinen) rengas, ts. kaikki (kommutatiivisen) renkaan
ehdot periytyvät renkaalta 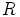 algebralle
algebralle 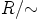 , jos
, jos 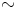 on kongruenssi.
on kongruenssi.
c) Osoita, että jos 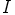 on renkaan
on renkaan 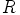 ihanne ja
ihanne ja 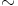 ehdolla
ehdolla
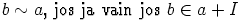 |
määritelty ekvivalenssirelaatio, niin  on kongruenssi.
on kongruenssi.
d) Osoita, että 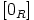 on renkaan
on renkaan 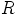 ihanne, jos
ihanne, jos 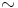 on kongruenssi.
on kongruenssi.