Ratkaisu:
a)  on parillinen, jos ja vain jos
on parillinen, jos ja vain jos 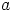 ja
ja 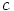 ovat joko molemmat
parillisia tai molemmat parittomia. Yksittäisessä luokassa siis kaikkien parien
ensimmäisten elementtien pariteetti on sama. Samoin toisten elementtien.
Siispä luokkia on kaikkiaan neljä ja niiden edustajiksi kelpaavat vaikkapa
parit
ovat joko molemmat
parillisia tai molemmat parittomia. Yksittäisessä luokassa siis kaikkien parien
ensimmäisten elementtien pariteetti on sama. Samoin toisten elementtien.
Siispä luokkia on kaikkiaan neljä ja niiden edustajiksi kelpaavat vaikkapa
parit 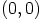 ,
, 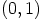 ,
, 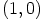 ja
ja 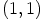 .
.
b) Determinantti voi tietenkin olla mikä tahansa kokonaisluku. Niinpä
luokkia on ”yhtä paljon” kuin reaalilukujakin. Determinantti on helpointa
laskea lävistäjämatriisista, joten edustajistoksi kannattaa valita vaikkapa
joukko 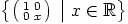 .
.
 on parillinen, jos ja vain jos
on parillinen, jos ja vain jos 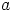 ja
ja 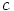 ovat joko molemmat
parillisia tai molemmat parittomia. Yksittäisessä luokassa siis kaikkien parien
ensimmäisten elementtien pariteetti on sama. Samoin toisten elementtien.
Siispä luokkia on kaikkiaan neljä ja niiden edustajiksi kelpaavat vaikkapa
parit
ovat joko molemmat
parillisia tai molemmat parittomia. Yksittäisessä luokassa siis kaikkien parien
ensimmäisten elementtien pariteetti on sama. Samoin toisten elementtien.
Siispä luokkia on kaikkiaan neljä ja niiden edustajiksi kelpaavat vaikkapa
parit 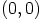 ,
, 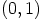 ,
, 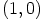 ja
ja 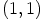 .
.
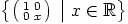 .
.