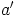 ja
ja 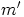 ne luvut, joilla
ne luvut, joilla 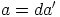 ,
, 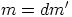 ja
ja
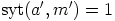 .
.
Ratkaisu: Olkoot 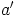 ja
ja 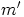 ne luvut, joilla
ne luvut, joilla 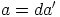 ,
, 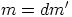 ja
ja
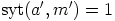 .
.
Oletetaan ensin, että 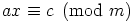 on ratkeava. Silloin on olemassa sellainen
luku
on ratkeava. Silloin on olemassa sellainen
luku 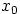 , että
, että 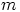 ja edelleen
ja edelleen 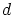 jakaa luvun
jakaa luvun 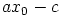 . Koska
. Koska 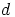 jakaa myös
luvun
jakaa myös
luvun 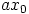 , jakaa se siis myös luvun
, jakaa se siis myös luvun 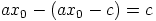 .
.
Oletetaan toiseksi, että 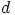 jakaa luvun
jakaa luvun 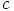 , eli on olemassa luku
, eli on olemassa luku 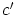 , jolla
, jolla
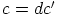 . Koska
. Koska 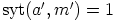 , on yhtälöllä
, on yhtälöllä 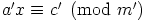 ratkaisu
ratkaisu 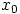 ,
eli
,
eli 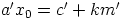 , jollakin luvulla
, jollakin luvulla 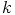 . Silloin
. Silloin
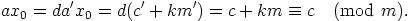 |
Edellä nähtiin, että jos 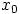 on yhtälön
on yhtälön 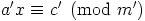 ratkaisu, on se myös
alkuperäisen yhtälön
ratkaisu, on se myös
alkuperäisen yhtälön 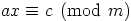 ratkaisu. Tämä pätee myös kääntäen.
Jos nimittäin
ratkaisu. Tämä pätee myös kääntäen.
Jos nimittäin 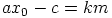 , eli
, eli 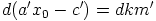 , niin jakamalla
puolittain luvulla
, niin jakamalla
puolittain luvulla 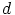 nähdään, että
nähdään, että 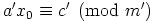 . Yhtälöillä on
siis samat ratkaisut. Yhtälöllä
. Yhtälöillä on
siis samat ratkaisut. Yhtälöllä 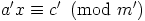 on yksikäsitteinen
ratkaisu
on yksikäsitteinen
ratkaisu 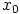 välillä
välillä 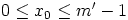 , joten yhtälöiden kaikki ratkaisut
muodostavat joukon
, joten yhtälöiden kaikki ratkaisut
muodostavat joukon 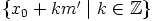 . Näistä ratkaisuista osuvat välille
. Näistä ratkaisuista osuvat välille
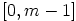 luvut
luvut 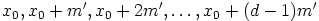 , joita on
, joita on 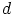 kappaletta.
kappaletta.