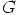 olisi korkeintaan kaksi eri
aliryhmää. Näiden täytyisi silloin olla
olisi korkeintaan kaksi eri
aliryhmää. Näiden täytyisi silloin olla 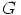 itse ja
itse ja  (jotka voivat olla samoja,
jos
(jotka voivat olla samoja,
jos 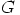 on triviaali ryhmä). Silloin
on triviaali ryhmä). Silloin
Ratkaisu: Oletetaan kääntäen, että ryhmällä 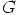 olisi korkeintaan kaksi eri
aliryhmää. Näiden täytyisi silloin olla
olisi korkeintaan kaksi eri
aliryhmää. Näiden täytyisi silloin olla 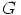 itse ja
itse ja  (jotka voivat olla samoja,
jos
(jotka voivat olla samoja,
jos 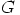 on triviaali ryhmä). Silloin
on triviaali ryhmä). Silloin
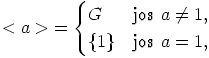 |
eli 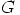 on syklinen, jolloin se on myös kommutatiivinen.
on syklinen, jolloin se on myös kommutatiivinen.
Huomaa, että käänteinen väite ei pidä paikkaansa: ryhmä voi olla kommutatiivinen,
vaikka sillä olisikin vähintään kolme eri aliryhmää. Ajattele vaikkapa ryhmää
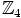 , jolla on aliryhmä
, jolla on aliryhmä 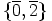 .
.