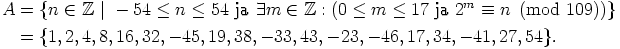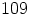 on alkuluku, on
on alkuluku, on 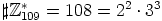 , joten Lagrangen
lauseen mukaan alkion
, joten Lagrangen
lauseen mukaan alkion  kertaluku
kertaluku 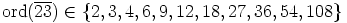 .
Kertaluvun määrittämiseksi lasketaan aluksi
.
Kertaluvun määrittämiseksi lasketaan aluksi
Ratkaisu: Koska 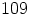 on alkuluku, on
on alkuluku, on 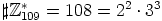 , joten Lagrangen
lauseen mukaan alkion
, joten Lagrangen
lauseen mukaan alkion  kertaluku
kertaluku 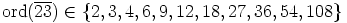 .
Kertaluvun määrittämiseksi lasketaan aluksi
.
Kertaluvun määrittämiseksi lasketaan aluksi
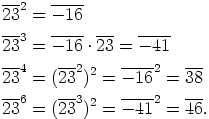
Sitten ei jatketakaan tämän pidemmälle, koska huomataan, että
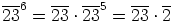 , mistä seuraa supistussäännön avulla (tai siis kertomalla
yhtälö puolittain vasemmalta alkiolla
, mistä seuraa supistussäännön avulla (tai siis kertomalla
yhtälö puolittain vasemmalta alkiolla 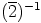 )
)
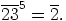 |
Seuraavaksi havaitaan, että
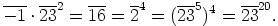 |
Kun tässä supistetaan oikealta alkiolla 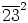 , saadaan
, saadaan 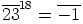 , eli
, eli 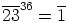 .
Siispä alkion
.
Siispä alkion 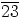 kertaluku ei voi olla ainakaan suurempi kuin 36. Osoitetaan,
ettei se ole myöskään pienempi.
kertaluku ei voi olla ainakaan suurempi kuin 36. Osoitetaan,
ettei se ole myöskään pienempi. 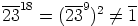 , joten
, joten 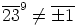 . Tästä
seuraa, että
. Tästä
seuraa, että
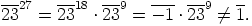 |
Suoraan laskemalla saadaan
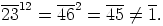 |
Saadaan siis 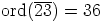 .
.
Nyt 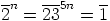 , jos ja vain jos luku
, jos ja vain jos luku  jakaa luvun
jakaa luvun 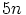 , jos ja vain jos luku
, jos ja vain jos luku
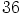 jakaa luvun
jakaa luvun 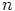 . Siispä myös
. Siispä myös 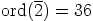 , eli
, eli 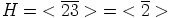 . Koska
. Koska
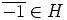 , niin
, niin
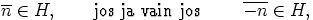 |
kaikilla luvuilla 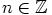 . Saadaan
. Saadaan 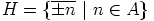 , missä
, missä