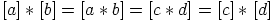 .
.
Ratkaisu:
a) Kongruenssiehdosta saadaan suoraan laskemalla
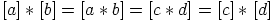 .
.
b) Ryhmäehtojen osoittamiseksi oletetaan, että alkiot 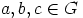 on valittu
mielivaltaisesti. Suoraan laskemalla saadaan
on valittu
mielivaltaisesti. Suoraan laskemalla saadaan
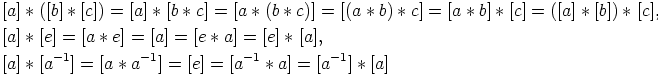
sekä kommutatiivisen ryhmän tapauksessa vielä
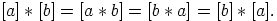 |
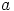 ,
, 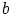 ja
ja 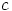 oli valittu mielivaltaisesti, toimivat yllä olevat ehdot
tietenkin kaikille ryhmän
oli valittu mielivaltaisesti, toimivat yllä olevat ehdot
tietenkin kaikille ryhmän 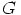 alkioille ja siis kaikille ryhmän
alkioille ja siis kaikille ryhmän 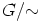 luokille. Siispä
ryhmän
luokille. Siispä
ryhmän 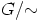 neutraaliluokka on
neutraaliluokka on  ja luokan
ja luokan 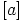 käänteisluokka
käänteisluokka
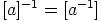 . Huomaa, että kaikki laskut ryhmässä
. Huomaa, että kaikki laskut ryhmässä 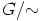 palautuvat laskuiksi
ryhmässä
palautuvat laskuiksi
ryhmässä 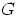 .
.
c) Olkoon 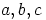 ja
ja 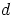 mielivaltaisesti valittuja ryhmän
mielivaltaisesti valittuja ryhmän 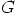 alkioita ja oletetaan,
että
alkioita ja oletetaan,
että 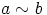 ja
ja 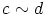 . Silloin
. Silloin 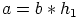 ja
ja 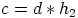 , joillakin ryhmän
, joillakin ryhmän 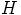 alkioilla
alkioilla 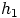 ja
ja 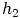 . Koska
. Koska 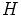 on normaali aliryhmä, on
on normaali aliryhmä, on 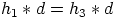 , jollakin
alkiolla
, jollakin
alkiolla 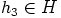 . Nyt saadaan
. Nyt saadaan
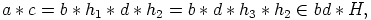 |
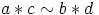 . Koska kongruenssiehto toimii mielivaltaisesti valituille alkioille,
toimii se silloin kaikille ryhmän
. Koska kongruenssiehto toimii mielivaltaisesti valituille alkioille,
toimii se silloin kaikille ryhmän 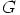 alkioille. Siispä
alkioille. Siispä  on kongruenssi.
on kongruenssi.
d) Osoitetaan ensin aliryhmäkriteerin avulla, että  on ryhmän
on ryhmän 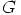 aliryhmä.
Luonnollisesti
aliryhmä.
Luonnollisesti 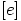 on epätyhjä, koska ainakin
on epätyhjä, koska ainakin 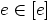 . Oletetaan sitten, että
. Oletetaan sitten, että
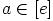 ja
ja 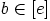 . Silloin relaation
. Silloin relaation 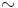 refleksiivisyydestä ja kongruenssiehdosta
saadaan
refleksiivisyydestä ja kongruenssiehdosta
saadaan
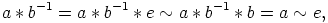 |
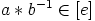 . Siispä ainakin
. Siispä ainakin  on ryhmän
on ryhmän 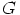 aliryhmä.
Osoitetaan vielä normaalius. Olkoon
aliryhmä.
Osoitetaan vielä normaalius. Olkoon 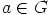 ja
ja 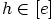 mielivaltaisesti valittuja
alkioita. Koska
mielivaltaisesti valittuja
alkioita. Koska  on ekvivalenssirelaatio on
on ekvivalenssirelaatio on 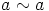 ja
ja 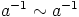 .
Silloin kongruenssiehdon avulla saadaan ensin
.
Silloin kongruenssiehdon avulla saadaan ensin 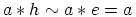 ja sitten
ja sitten
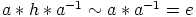 , eli
, eli 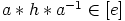 . Jälleen tämä päättely toimii yhtä
hyvin kaikilla alkioilla
. Jälleen tämä päättely toimii yhtä
hyvin kaikilla alkioilla 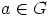 ja
ja 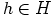 , jolloin aliryhmän normaalisuuskriteerin
perusteella
, jolloin aliryhmän normaalisuuskriteerin
perusteella 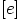 on ryhmän
on ryhmän 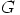 normaali aliryhmä.
normaali aliryhmä.