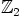 ja
ja 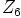 ovat Abelin ryhmiä, joten samoin on niiden karteesinen
tulo
ovat Abelin ryhmiä, joten samoin on niiden karteesinen
tulo 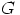 . Nimittäin
. Nimittäin
Ratkaisu:
a) Ryhmät 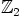 ja
ja 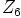 ovat Abelin ryhmiä, joten samoin on niiden karteesinen
tulo
ovat Abelin ryhmiä, joten samoin on niiden karteesinen
tulo 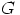 . Nimittäin
. Nimittäin
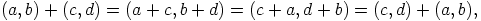 |
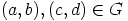 . Toisaalta kaikki Abelin ryhmän aliryhmät ovat
normaaleja.
. Toisaalta kaikki Abelin ryhmän aliryhmät ovat
normaaleja.
b) 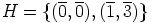 , koska
, koska 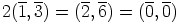 .
.
c) Huomaa aluksi, että
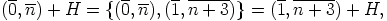 |
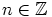 . Niinpä edustajistoksi
. Niinpä edustajistoksi 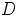 voidaan valita joukko
voidaan valita joukko
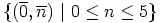 .
.
d) Valitun edustajiston 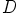 ansiosta laskeminen ryhmässä
ansiosta laskeminen ryhmässä 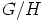 on nyt helppoa.
Nimittäin
on nyt helppoa.
Nimittäin
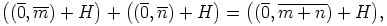 |
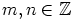 .
.
e) Kohdasta d) nähdään välittömästi, että ryhmä 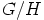 on isomorfinen
ryhmän
on isomorfinen
ryhmän 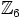 kanssa, joten
kanssa, joten 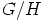 on syklinen.
on syklinen.