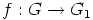 .
.
Ratkaisu: Voidaan olettaa, että kyseinen isomorfismi on 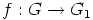 .
.
a) Olkoon alkiot 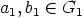 valittu mielivaltaisesti. Koska
valittu mielivaltaisesti. Koska 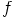 on surjektio, on
olemassa jotkin alkiot
on surjektio, on
olemassa jotkin alkiot 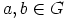 , jotka ovat alkioiden
, jotka ovat alkioiden 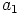 ja
ja 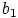 alkukuvia, eli
alkukuvia, eli
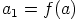 ja
ja 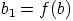 . Silloin
. Silloin
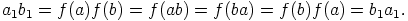 |
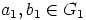 , koska se pätee mielivaltaisesti
valituillekin. Siispä
, koska se pätee mielivaltaisesti
valituillekin. Siispä 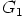 on kommutatiivinen.
on kommutatiivinen.
b) Olkoon  ja
ja 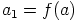 . Osoitetaan, että
. Osoitetaan, että  . Olkoon
siis
. Olkoon
siis 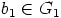 valittu mielivaltaisesti. Silloin on olemassa alkio
valittu mielivaltaisesti. Silloin on olemassa alkio  ,
jonka kuva
,
jonka kuva 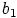 on. Nyt on olemassa jokin luku
on. Nyt on olemassa jokin luku 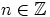 , jolla
, jolla 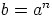 .
Saadaan
.
Saadaan
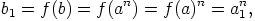 |
 . Jälleen edellä sanottu pätee kaikille alkioille
. Jälleen edellä sanottu pätee kaikille alkioille 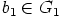 , joten
, joten
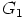 on syklinen.
on syklinen.