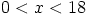 on
on 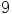 lukua
lukua 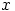 , jotka eivät ole kahdella jaollisia.
Näistä luvuista joka kolmas on kolmella jaollinen. Siispä välillä
, jotka eivät ole kahdella jaollisia.
Näistä luvuista joka kolmas on kolmella jaollinen. Siispä välillä 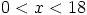 on
täsmälleen kuusi lukua
on
täsmälleen kuusi lukua 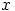 jotka ovat jaottomia sekä kahdella että kolmella.
Niinpä
jotka ovat jaottomia sekä kahdella että kolmella.
Niinpä 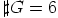 ja
ja
Ratkaisu: Välillä 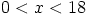 on
on 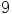 lukua
lukua 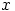 , jotka eivät ole kahdella jaollisia.
Näistä luvuista joka kolmas on kolmella jaollinen. Siispä välillä
, jotka eivät ole kahdella jaollisia.
Näistä luvuista joka kolmas on kolmella jaollinen. Siispä välillä 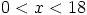 on
täsmälleen kuusi lukua
on
täsmälleen kuusi lukua 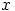 jotka ovat jaottomia sekä kahdella että kolmella.
Niinpä
jotka ovat jaottomia sekä kahdella että kolmella.
Niinpä 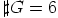 ja
ja
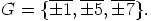 |
Minkä tahansa ryhmän 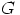 alkion kertaluku jakaa luvun
alkion kertaluku jakaa luvun 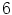 , eli kertaluku on
, eli kertaluku on
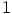 (ainoastaan alkiolla
(ainoastaan alkiolla 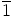 ),
), 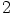 ,
, 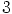 tai
tai 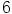 . Nyt
. Nyt 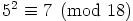 ja
ja
 , joten alkion
, joten alkion 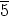 kertaluku ei ole mikään luvuista
kertaluku ei ole mikään luvuista 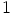 ,
,
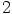 tai
tai 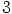 , eli sen täytyy olla
, eli sen täytyy olla 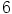 . Siispä
. Siispä  .
.
Selvästi kuvaus 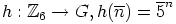 on isomorfismi. Ryhmän
on isomorfismi. Ryhmän 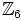 aliryhmät
ovat
aliryhmät
ovat  ,
, 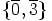 ,
, 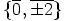 ja
ja 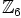 itse. Ryhmän
itse. Ryhmän 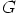 aliryhmät ovat silloin
täsmälleen ryhmän
aliryhmät ovat silloin
täsmälleen ryhmän 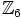 aliryhmien
aliryhmien 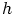 -kuvat:
-kuvat:  ,
,  ,
,
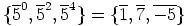 ja
ja 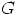 .
.