Ratkaisu:
a) Alirenkaan määritelmästä nähdään, että on löydettävä sellainen rengas
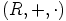 , jolla on yhtälön
, jolla on yhtälön 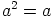 toteuttava alkio
toteuttava alkio 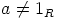 , joka toimii renkaan
, joka toimii renkaan
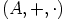 ykkösalkiona
ykkösalkiona 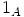 . Itse asiassa tällöin voidaan valita
. Itse asiassa tällöin voidaan valita 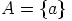 , eli
, eli
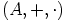 on nollarengas. Tässä ei kannata mennä merta edemmäs kalaan, eli
riittää valita
on nollarengas. Tässä ei kannata mennä merta edemmäs kalaan, eli
riittää valita 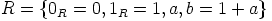 . Oletetaan vielä, että
. Oletetaan vielä, että 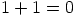 ja
ja 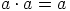 . Näistä yhtälöistä saadaan yhteenlaskun kommutatiivisuuden ja
distributiivilain avulla
. Näistä yhtälöistä saadaan yhteenlaskun kommutatiivisuuden ja
distributiivilain avulla 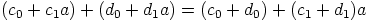 ja
ja
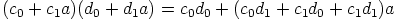 ,
, 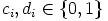 ,
, 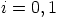 .
Alla on yhteen- ja kertolaskutaulut:
.
Alla on yhteen- ja kertolaskutaulut:
Osoitetaan vielä kertolaskun assosiatiivisuus. Oletetaan, että 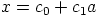 ,
,
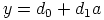 ja
ja 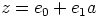 ,
, 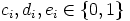 ,
, 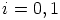 . Saadaan
. Saadaan

Distributiivisuus voidaan osoittaa samaan tapaan ja yhteenlaskun assosiatiivisuus
ja kommutatiivisuus ovat triviaaleja.
b) Nyt on puolestaan löydettävä sellainen rengas 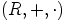 , jolla on yhtälöt
, jolla on yhtälöt
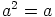 ja
ja 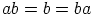 toteuttavat alkiot
toteuttavat alkiot 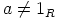 ja
ja 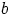 . Nyt voidaan valita
. Nyt voidaan valita
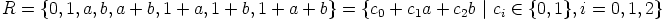 ,
jossa
,
jossa 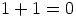 ,
, 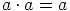 ja
ja  . Näistä yhtälöistä
saadaan
. Näistä yhtälöistä
saadaan
ja
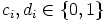 ,
, 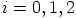 . Yhteenlaskutaulu on
ja kertolaskutaulu
Distributiivisuus ja operaatioiden assosiatiivisuudet voidaan todistaa samaan
tapaan kuin a)-kohdassa. Saadaan
. Yhteenlaskutaulu on
ja kertolaskutaulu
Distributiivisuus ja operaatioiden assosiatiivisuudet voidaan todistaa samaan
tapaan kuin a)-kohdassa. Saadaan 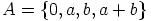 , missä
, missä  .
.
c) Yleistetään edellä saadut tulokset. Olkoon 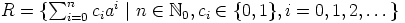 ,
missä
,
missä 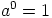 ,
, 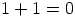 ,
, 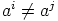 , jos
, jos 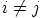 , ja
, ja 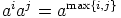 . Oletetaan,
että
. Oletetaan,
että 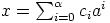 ,
, 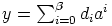 ja
ja 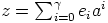 . Tässä voidaan olettaa,
että
. Tässä voidaan olettaa,
että 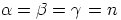 lisäämällä alkioiden perään tarvittaessa nollatermejä. Nyt
yhteen- ja kertolasku näyttävät seuraavanlaisilta:
lisäämällä alkioiden perään tarvittaessa nollatermejä. Nyt
yhteen- ja kertolasku näyttävät seuraavanlaisilta:
Nähdään, että
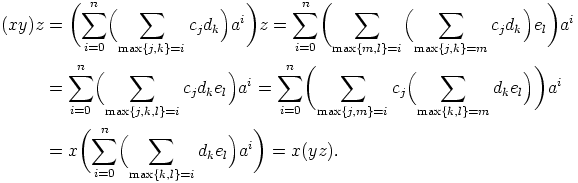
Muiden ehtojen todistaminen on suoraviivaista. Huomataan, että
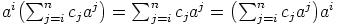 , Joten
, Joten 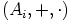 , missä
, missä
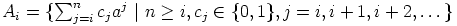 , on rengas ja
, on rengas ja
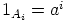 .
.
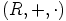 , jolla on yhtälön
, jolla on yhtälön 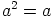 toteuttava alkio
toteuttava alkio 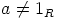 , joka toimii renkaan
, joka toimii renkaan
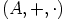 ykkösalkiona
ykkösalkiona 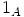 . Itse asiassa tällöin voidaan valita
. Itse asiassa tällöin voidaan valita 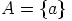 , eli
, eli
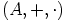 on nollarengas. Tässä ei kannata mennä merta edemmäs kalaan, eli
riittää valita
on nollarengas. Tässä ei kannata mennä merta edemmäs kalaan, eli
riittää valita 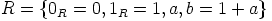 . Oletetaan vielä, että
. Oletetaan vielä, että 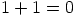 ja
ja 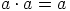 . Näistä yhtälöistä saadaan yhteenlaskun kommutatiivisuuden ja
distributiivilain avulla
. Näistä yhtälöistä saadaan yhteenlaskun kommutatiivisuuden ja
distributiivilain avulla 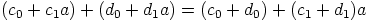 ja
ja
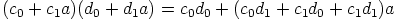 ,
, 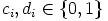 ,
, 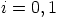 .
Alla on yhteen- ja kertolaskutaulut:
.
Alla on yhteen- ja kertolaskutaulut:
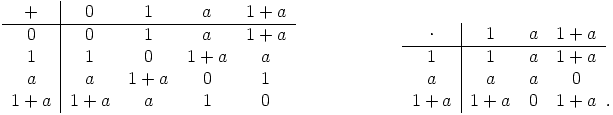
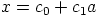 ,
,
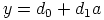 ja
ja 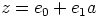 ,
, 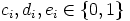 ,
, 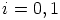 . Saadaan
. Saadaan

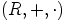 , jolla on yhtälöt
, jolla on yhtälöt
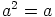 ja
ja 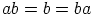 toteuttavat alkiot
toteuttavat alkiot 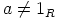 ja
ja 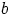 . Nyt voidaan valita
. Nyt voidaan valita
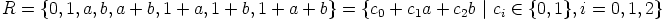 ,
jossa
,
jossa 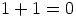 ,
, 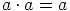 ja
ja  . Näistä yhtälöistä
saadaan
. Näistä yhtälöistä
saadaan
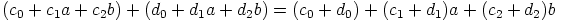
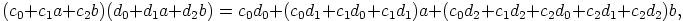
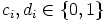 ,
, 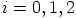 . Yhteenlaskutaulu on
. Yhteenlaskutaulu on


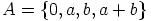 , missä
, missä  .
.
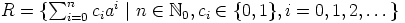 ,
missä
,
missä 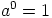 ,
, 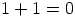 ,
, 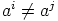 , jos
, jos 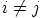 , ja
, ja 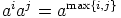 . Oletetaan,
että
. Oletetaan,
että 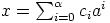 ,
, 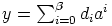 ja
ja 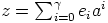 . Tässä voidaan olettaa,
että
. Tässä voidaan olettaa,
että 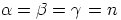 lisäämällä alkioiden perään tarvittaessa nollatermejä. Nyt
yhteen- ja kertolasku näyttävät seuraavanlaisilta:
lisäämällä alkioiden perään tarvittaessa nollatermejä. Nyt
yhteen- ja kertolasku näyttävät seuraavanlaisilta:
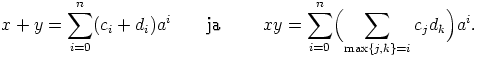
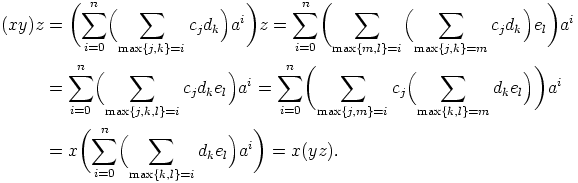
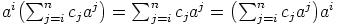 , Joten
, Joten 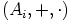 , missä
, missä
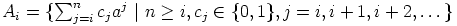 , on rengas ja
, on rengas ja
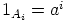 .
.