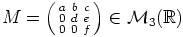 ja
ja 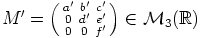 tulo:
tulo:
Ratkaisu: Lasketaan ensin kahden mielivaltaisesti valitun yläkolmiomatriisin
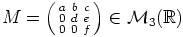 ja
ja 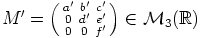 tulo:
tulo:
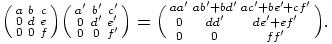 |
Huomataan, että yläkolmiomatriisien tulo säilyy yläkolmiomatriisina. Itse asiassa
kaikki joukot 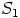 ,
, 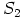 sekä
sekä 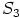 ovat suljettuja kertolaskun suhteen.
ovat suljettuja kertolaskun suhteen. 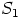 ei
kuitenkaan ole suljettu yhteenlaskun suhteen, koska esimerkiksi
ei
kuitenkaan ole suljettu yhteenlaskun suhteen, koska esimerkiksi 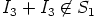 .
Niinpä
.
Niinpä 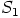 ei ole alirengas.
ei ole alirengas. 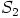 ei myöskään ole, sillä renkaan
ei myöskään ole, sillä renkaan 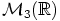 ykkösalkio
ykkösalkio 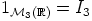 ei kuulu siihen. Sen sijaan
ei kuulu siihen. Sen sijaan 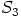 on kertolaskun lisäksi
suljettu yhteenlaskun suhteen, sisältää kaikkien alkioidensa
on kertolaskun lisäksi
suljettu yhteenlaskun suhteen, sisältää kaikkien alkioidensa 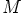 vasta-alkiot
vasta-alkiot
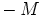 ja myös identiteettimatriisi kuuluu siihen. Niinpä alirengaskriteeristä
seuraa, että
ja myös identiteettimatriisi kuuluu siihen. Niinpä alirengaskriteeristä
seuraa, että 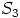 on alirengas.
on alirengas.