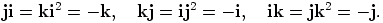
Ratkaisu:
a)
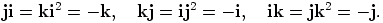 |
b) Distributiivilaista ja a-kohdasta seuraa
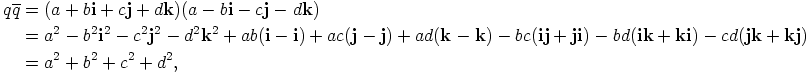
aina kun 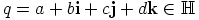 .
.
c) b-kohdan mukaan 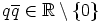 , kaikilla
, kaikilla 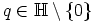 . Niinpä alkion
. Niinpä alkion
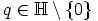 käänteisalkio on
käänteisalkio on 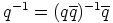 .
.
d) Käytetään alirengaskriteeriä. Ensinnäkin ykkösalkio eli identiteettimatriisi
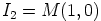 kuuluu triviaalisti joukkoon
kuuluu triviaalisti joukkoon 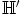 . Oletetaan, että matriisit
. Oletetaan, että matriisit
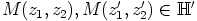 on valittu mielivaltaisesti. Silloin
on valittu mielivaltaisesti. Silloin
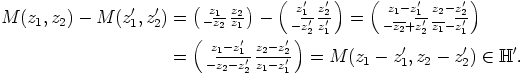
Kolmanneksi
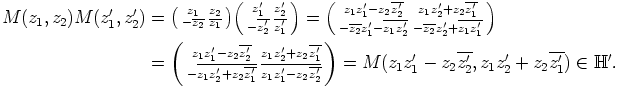
e) Olkoon kuvaus 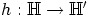 ,
, 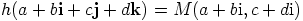 . Selvästi
. Selvästi
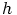 on bijektio. Näytetään, että se on homomorfismi, eli isomorfismi. Oletetaan,
että alkiot
on bijektio. Näytetään, että se on homomorfismi, eli isomorfismi. Oletetaan,
että alkiot 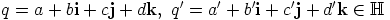 on valittu
mielivaltaisesti. Silloin ensinnäkin
on valittu
mielivaltaisesti. Silloin ensinnäkin
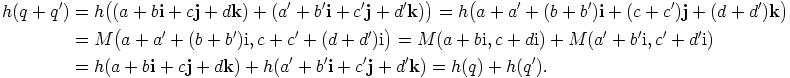
Toiseksi d-kohdan avulla saadaan
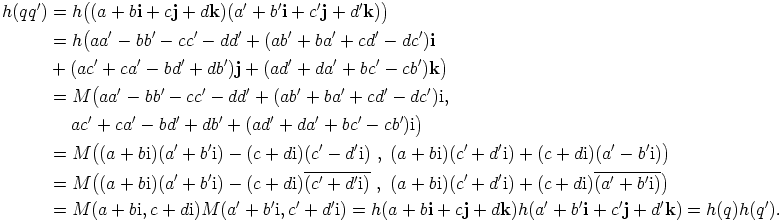
Kolmanneksi
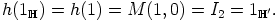 |