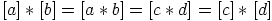 .
.
Ratkaisu:
a) Kongruenssiehdosta saadaan suoraan laskemalla
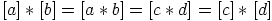 .
.
b) Kohdasta a) seuraa, että operaatiot  ja
ja  ovat hyvinmääritellyt
myös joukolle
ovat hyvinmääritellyt
myös joukolle 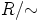 . Renkaan
. Renkaan 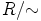 laskulait palautuvat renkaan
laskulait palautuvat renkaan 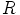 laeiksi. Renkaassa
laeiksi. Renkaassa 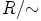 on
on 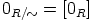 ja
ja 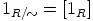 sekä luokan
sekä luokan 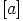 käänteisluokka
käänteisluokka 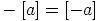 . Näytetään esimerkiksi distributiivilaki. Oletetaan,
että alkiot
. Näytetään esimerkiksi distributiivilaki. Oletetaan,
että alkiot 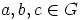 on valittu mielivaltaisesti. Saadaan
on valittu mielivaltaisesti. Saadaan
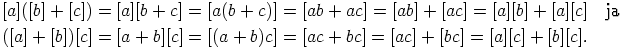
Koska alkiot 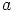 ,
, 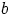 ja
ja 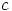 oli valittu mielivaltaisesti, toimivat yllä olevat
ehdot tietenkin kaikille renkaan
oli valittu mielivaltaisesti, toimivat yllä olevat
ehdot tietenkin kaikille renkaan 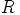 alkioille ja siis kaikille renkaan
alkioille ja siis kaikille renkaan 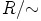 luokille.
luokille.
c) Olkoon 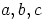 ja
ja 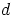 mielivaltaisesti valittuja renkaan
mielivaltaisesti valittuja renkaan 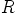 alkioita ja
oletetaan, että
alkioita ja
oletetaan, että 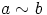 ja
ja 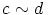 . Silloin
. Silloin 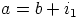 ja
ja 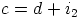 , joillakin
ihanteen
, joillakin
ihanteen 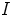 alkioilla
alkioilla 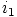 ja
ja 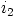 . Koska
. Koska 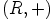 on kommutatiivinen ryhmä
saadaan
on kommutatiivinen ryhmä
saadaan
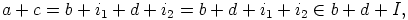 |
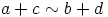 . Koska
. Koska 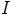 on ihanne, niin
on ihanne, niin 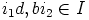 . Nyt saadaan
. Nyt saadaan
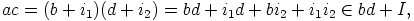 |
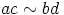 . Koska kongruenssiehto toimii mielivaltaisesti valituille alkioille,
toimii se silloin kaikille renkaan
. Koska kongruenssiehto toimii mielivaltaisesti valituille alkioille,
toimii se silloin kaikille renkaan 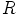 alkioille. Siispä
alkioille. Siispä 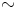 on kongruenssi.
on kongruenssi.
d) Osoitetaan väite Ihannekriteerin avulla. Luonnollisesti 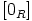 on epätyhjä,
koska ainakin
on epätyhjä,
koska ainakin 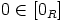 . Oletetaan sitten, että
. Oletetaan sitten, että 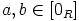 ja
ja 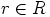 . Silloin
relaation
. Silloin
relaation 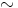 refleksiivisyydestä ja kongruenssiehdosta saadaan
refleksiivisyydestä ja kongruenssiehdosta saadaan
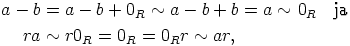
eli 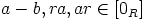 . Siispä
. Siispä 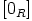 on renkaan
on renkaan 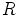 ihanne.
ihanne.