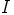 jokin mielivaltaisesti valittu, nollasta eroava, renkaan
jokin mielivaltaisesti valittu, nollasta eroava, renkaan 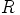 ihanne ja
ihanne ja 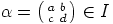 nollamatriisista eroava matriisi. Määritetään aluksi
neljä ihanteesta
nollamatriisista eroava matriisi. Määritetään aluksi
neljä ihanteesta 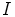 löytyvää matriisia:
löytyvää matriisia:
Ratkaisu: Olkoon 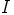 jokin mielivaltaisesti valittu, nollasta eroava, renkaan
jokin mielivaltaisesti valittu, nollasta eroava, renkaan 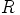 ihanne ja
ihanne ja 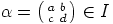 nollamatriisista eroava matriisi. Määritetään aluksi
neljä ihanteesta
nollamatriisista eroava matriisi. Määritetään aluksi
neljä ihanteesta 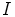 löytyvää matriisia:
löytyvää matriisia:
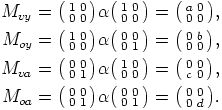
Nyt huomataan, että esimerkiksi  , jos ja vain jos
, jos ja vain jos 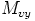 on nollamatriisi.
Samoin
on nollamatriisi.
Samoin  , jos ja vain jos
, jos ja vain jos 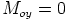 , jne. Niinpä ainakin yksi näistä neljästä
matriisista
, jne. Niinpä ainakin yksi näistä neljästä
matriisista 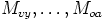 eroaa nollamatriisista. Oletetaan nyt esimerkiksi, että
eroaa nollamatriisista. Oletetaan nyt esimerkiksi, että
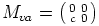 poikkeaa nollamatriisista (muut tapaukset käsitellään vastaavasti).
On helppo havaita, että jos jotakin matriisia kerrotaan vasemmalta matriisilla
poikkeaa nollamatriisista (muut tapaukset käsitellään vastaavasti).
On helppo havaita, että jos jotakin matriisia kerrotaan vasemmalta matriisilla
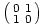 , vaihtavat sen vaakarivit paikkoja. Vastaavasti oikealta kertomalla
vaihtavat pystysarakkeet paikkoja. Niinpä löydetään kaksi uutta ihanteen
, vaihtavat sen vaakarivit paikkoja. Vastaavasti oikealta kertomalla
vaihtavat pystysarakkeet paikkoja. Niinpä löydetään kaksi uutta ihanteen 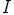 matriisia:
matriisia:
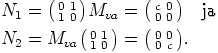
Nyt säännöllinen diagonaalimatriisi 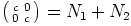 kuuluu ihanteeseen
kuuluu ihanteeseen 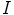 , jolloin
myös identiteettimatriisi, eli renkaan
, jolloin
myös identiteettimatriisi, eli renkaan 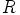 ykkösalkio,
ykkösalkio, 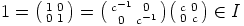 .
Silloin
.
Silloin 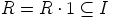 , eli
, eli 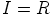 . Koska
. Koska 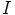 , ja samalla
, ja samalla  , oli valittu
mielivaltaisesti, ei renkaassa
, oli valittu
mielivaltaisesti, ei renkaassa 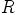 ole muita ihanteita triviaalien ihanteiden
ole muita ihanteita triviaalien ihanteiden  ja
ja
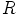 lisäksi.
lisäksi.