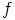 mikä tahansa ryhmähomomorfismi
ja
mikä tahansa ryhmähomomorfismi
ja 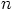 mikä tahansa kokonaisluku, niin
mikä tahansa kokonaisluku, niin 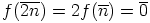 . Edelleen
. Edelleen
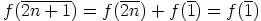 . Niinpä on olemassa vain kaksi erisuurta
ryhmähomomorfismia
. Niinpä on olemassa vain kaksi erisuurta
ryhmähomomorfismia 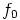 ja
ja 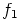 , missä
, missä 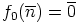 , kaikilla
, kaikilla 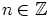 , ja
, ja
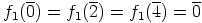 sekä
sekä 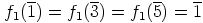 .
.
Ratkaisu:
a) Aluksi
kannattaa pistää merkille, että olipa 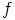 mikä tahansa ryhmähomomorfismi
ja
mikä tahansa ryhmähomomorfismi
ja 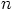 mikä tahansa kokonaisluku, niin
mikä tahansa kokonaisluku, niin 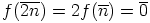 . Edelleen
. Edelleen
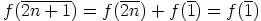 . Niinpä on olemassa vain kaksi erisuurta
ryhmähomomorfismia
. Niinpä on olemassa vain kaksi erisuurta
ryhmähomomorfismia 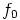 ja
ja 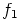 , missä
, missä 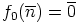 , kaikilla
, kaikilla 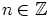 , ja
, ja
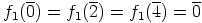 sekä
sekä 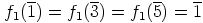 .
.
b) Ainoastaan 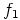 kuvaa ykkösalkion ykkösalkioksi. Myöskin
kuvaa ykkösalkion ykkösalkioksi. Myöskin
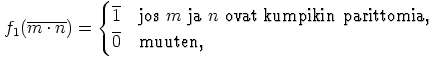 |
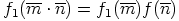 . Siispä ainoastaan
. Siispä ainoastaan 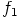 on rengashomomorfismi.
on rengashomomorfismi.
c) Oletetaan, että 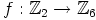 on jokin ryhmähomomorfismi. Silloin
on jokin ryhmähomomorfismi. Silloin
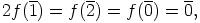 |
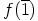 on joko
on joko 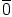 tai
tai 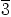 . Näin ryhmähomomorfismeja on jälleen vain kaksi
kappaletta. Kumpikaan ei kuvaa ykkösalkiota ykkösalkioksi, eikä siis ole
rengashomomorfismi.
. Näin ryhmähomomorfismeja on jälleen vain kaksi
kappaletta. Kumpikaan ei kuvaa ykkösalkiota ykkösalkioksi, eikä siis ole
rengashomomorfismi.