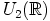 on renkaan
on renkaan  alirengas.
Ensinnäkin
alirengas.
Ensinnäkin 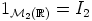 kuuluu joukkoon
kuuluu joukkoon 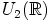 . Toiseksi yläkolmiomatriisien
erotus on triviaalisti edelleen yläkolmiomatriisi. Lasketaan vielä yläkolmiomatriisien
tulo:
. Toiseksi yläkolmiomatriisien
erotus on triviaalisti edelleen yläkolmiomatriisi. Lasketaan vielä yläkolmiomatriisien
tulo:
Ratkaisu:
a) Näytetään alirengaskriteerillä, että 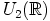 on renkaan
on renkaan  alirengas.
Ensinnäkin
alirengas.
Ensinnäkin 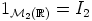 kuuluu joukkoon
kuuluu joukkoon 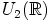 . Toiseksi yläkolmiomatriisien
erotus on triviaalisti edelleen yläkolmiomatriisi. Lasketaan vielä yläkolmiomatriisien
tulo:
. Toiseksi yläkolmiomatriisien
erotus on triviaalisti edelleen yläkolmiomatriisi. Lasketaan vielä yläkolmiomatriisien
tulo:
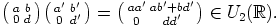 |
b) Nolla-alkiona toimii 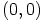 ja ykkösalkiona
ja ykkösalkiona 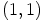 . Kaikki rengaspostulaattien
todistukset ovat suoraviivaisia laskuja. Näytetään esimerkkinä ensimmäinen
distributiivilaeista:
. Kaikki rengaspostulaattien
todistukset ovat suoraviivaisia laskuja. Näytetään esimerkkinä ensimmäinen
distributiivilaeista:
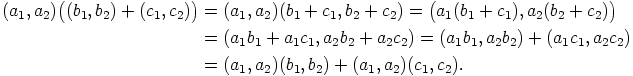
c) Oletetaan, että 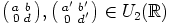 . Silloin
. Silloin
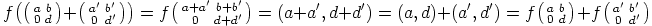 |
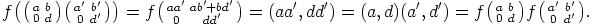 |
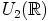 identiteettialkio
identiteettialkio 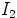 kuvautuu alkioksi
kuvautuu alkioksi 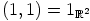 .
.
d) Matriisi 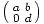 kuuluu ytimeen
kuuluu ytimeen
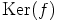 , jos ja vain jos
, jos ja vain jos 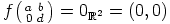 , jos ja vain jos
, jos ja vain jos 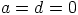 .
Siispä ytimeksi saadaan
.
Siispä ytimeksi saadaan 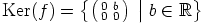 . Kuvaus
. Kuvaus 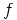 on selvästi
surjektio, eli kuvaksi
on selvästi
surjektio, eli kuvaksi 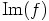 saadaan koko rengas
saadaan koko rengas 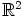 .
.
e) Renkaiden homomorfialauseesta saadaan nyt isomorfismi
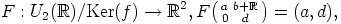 |
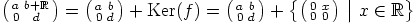 .
.
f) Joukko 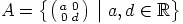 on triviaalisti renkaan
on triviaalisti renkaan 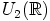 alirengas
(alirengaskriteeri). Kuvaus
alirengas
(alirengaskriteeri). Kuvaus 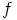 rajoitettuna tähän alirenkaaseen on selvästi
injektio ja surjektio, eli siis isomorfismi.
rajoitettuna tähän alirenkaaseen on selvästi
injektio ja surjektio, eli siis isomorfismi.