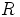 on kommutatiivinen ja että sen kaikilla
nollasta eroavilla alkioilla on käänteisalkio. Oletetaan siksi, että alkiot
on kommutatiivinen ja että sen kaikilla
nollasta eroavilla alkioilla on käänteisalkio. Oletetaan siksi, että alkiot 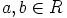 on valittu sattumanvaraisesti ja
on valittu sattumanvaraisesti ja 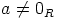 .
.
Ratkaisu: On osoitettava, että 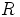 on kommutatiivinen ja että sen kaikilla
nollasta eroavilla alkioilla on käänteisalkio. Oletetaan siksi, että alkiot
on kommutatiivinen ja että sen kaikilla
nollasta eroavilla alkioilla on käänteisalkio. Oletetaan siksi, että alkiot 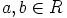 on valittu sattumanvaraisesti ja
on valittu sattumanvaraisesti ja 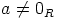 .
.
Alkion 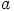 kertaluku additiivisessa ryhmässä
kertaluku additiivisessa ryhmässä 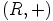 on suurempi kuin yksi, joten
sen täytyy olla
on suurempi kuin yksi, joten
sen täytyy olla 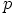 , koska Lagrangen lauseen seurauslauseen mukaan tämä
kertaluku jakaa ryhmän
, koska Lagrangen lauseen seurauslauseen mukaan tämä
kertaluku jakaa ryhmän 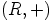 kertaluvun
kertaluvun 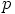 , joka oletettiin alkuluvuksi. Tämä
merkitsee sitä, että
, joka oletettiin alkuluvuksi. Tämä
merkitsee sitä, että 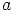 generoi ryhmän
generoi ryhmän 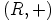 . Silloin on olemassa positiivinen
kokonaisluku
. Silloin on olemassa positiivinen
kokonaisluku 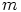 , jolla
, jolla 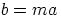 . Tällöin renkaan
. Tällöin renkaan 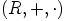 distributiivisuudesta
seuraa
distributiivisuudesta
seuraa
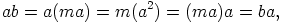 |
eli 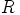 on kommutatiivinen rengas.
on kommutatiivinen rengas.
Koska 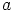 generoi ryhmän
generoi ryhmän 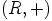 , on olemassa positiivinen kokonaisluku
, on olemassa positiivinen kokonaisluku
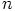 , jolla renkaan
, jolla renkaan 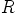 ykkösalkio on
ykkösalkio on 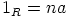 . Toisaalta renkaan
. Toisaalta renkaan 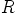 distributiivisuuden vuoksi
distributiivisuuden vuoksi
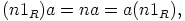 |
joten alkion 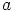 käänteisalkio on
käänteisalkio on 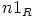 . Koska
. Koska 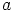 valittiin mielivaltaisesti, on siis
jokaisella renkaan
valittiin mielivaltaisesti, on siis
jokaisella renkaan 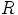 nollasta eroavalla alkiolla käänteisalkio.
nollasta eroavalla alkiolla käänteisalkio.