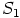 on itse asiassa rationaalilukujen kunta
on itse asiassa rationaalilukujen kunta 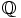 itse, sillä
itse, sillä
Ratkaisu:
a) 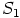 on itse asiassa rationaalilukujen kunta
on itse asiassa rationaalilukujen kunta 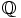 itse, sillä
itse, sillä
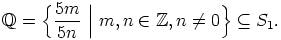 |
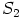 ei voi olla alirengas, sillä kunnan
ei voi olla alirengas, sillä kunnan 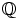 ykkösalkio, eli luku
ykkösalkio, eli luku 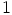 , ei kuulu siihen.
Joukkoihin
, ei kuulu siihen.
Joukkoihin 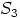 ja
ja  luku
luku 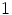 sen sijaan kuuluu. Lisäksi
sen sijaan kuuluu. Lisäksi
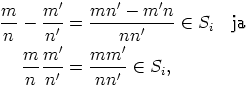
aina kun 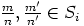 ,
, 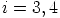 . Niinpä
. Niinpä 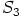 ja
ja 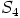 ovat molemmat alirenkaita.
Ne eivät kuitenkaan kumpikaan ole alikuntia, koska luvun
ovat molemmat alirenkaita.
Ne eivät kuitenkaan kumpikaan ole alikuntia, koska luvun 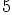 käänteisluku
käänteisluku 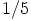 ei kuulu renkaaseen
ei kuulu renkaaseen 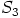 ja luvun
ja luvun  käänteisluku
käänteisluku 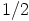 ei puolestaan kuulu
renkaaseen
ei puolestaan kuulu
renkaaseen  .
.
b) 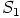 on kuntana triviaalisti myös lokaali rengas, sillä ainoa epäyksikkö
nolla muodostaa yksinään nollaihanteen. Renkaan
on kuntana triviaalisti myös lokaali rengas, sillä ainoa epäyksikkö
nolla muodostaa yksinään nollaihanteen. Renkaan 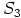 osalta havaitaan,
että
osalta havaitaan,
että
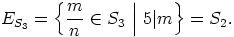 |
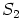 on ihannekriteerin mukaan ihanne, sillä se on epätyhjä sekä
on ihannekriteerin mukaan ihanne, sillä se on epätyhjä sekä
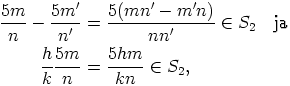
aina kun 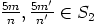 ja
ja 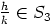 . Siispä
. Siispä 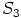 on myös lokaali rengas.
Sen sijaan
on myös lokaali rengas.
Sen sijaan 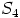 ei ole lokaali rengas, koska esimerkiksi luvut
ei ole lokaali rengas, koska esimerkiksi luvut 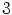 ja
ja 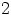 ovat
epäyksikköjä, eli kuuluvat joukkoon
ovat
epäyksikköjä, eli kuuluvat joukkoon 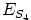 , mutta niiden erotus
, mutta niiden erotus 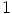 onkin yksikkö.
Jos nimittäin
onkin yksikkö.
Jos nimittäin 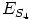 olisi ihanne, pitäisi myös tämän erotuksen kuulua
siihen.
olisi ihanne, pitäisi myös tämän erotuksen kuulua
siihen.
c) 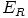 on maksimaalinen, jos ja vain jos jäännösluokkarengas
on maksimaalinen, jos ja vain jos jäännösluokkarengas 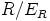 on kunta. Riittää siis näyttää, että mielivaltaisesti valitulla alkiolla
on kunta. Riittää siis näyttää, että mielivaltaisesti valitulla alkiolla
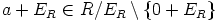 on käänteisalkio. Koska
on käänteisalkio. Koska 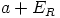 eroaa
nolla-alkiosta, niin
eroaa
nolla-alkiosta, niin 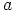 ei kuulu ihanteeseen
ei kuulu ihanteeseen 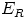 , eli alkiolla
, eli alkiolla 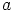 on
käänteisalkio
on
käänteisalkio 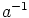 renkaassa
renkaassa 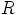 . Silloin alkion
. Silloin alkion 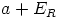 käänteisalkio
jäännösluokkarenkaassa
käänteisalkio
jäännösluokkarenkaassa 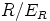 on luonnollisesti
on luonnollisesti  .
.