Ratkaisu:
a) Olkoon kuvaus 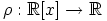 ,
, 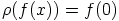 . Tämä kuvaus on selvästi
homomorfismi, koska renkaan ykkösalkio, vakiopolynomi
. Tämä kuvaus on selvästi
homomorfismi, koska renkaan ykkösalkio, vakiopolynomi 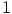 , kuvautuu
luvuksi
, kuvautuu
luvuksi 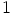 sekä kahden polynomin summan ja tulon arvot pisteessä nolla
ovat vastaavien polynomien nollapisteiden arvojen summa ja tulo.
Kuvauksen ytimen muodostavat ne polynomit, jotka saavat arvoksi nollan
pisteessä nolla. Nämä ovat täsmälleen ne polynomit, joiden vakiotermi on
nolla, eli jotka ovat jaollisia polynomilla
sekä kahden polynomin summan ja tulon arvot pisteessä nolla
ovat vastaavien polynomien nollapisteiden arvojen summa ja tulo.
Kuvauksen ytimen muodostavat ne polynomit, jotka saavat arvoksi nollan
pisteessä nolla. Nämä ovat täsmälleen ne polynomit, joiden vakiotermi on
nolla, eli jotka ovat jaollisia polynomilla 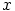 . Siis ydin on polynomin
. Siis ydin on polynomin  generoima ihanne.
Kuvaus
generoima ihanne.
Kuvaus 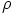 on selvästi surjektio, eli kuvaksi saadaan kunta. Tämä tarkoittaa
sitä, että
on selvästi surjektio, eli kuvaksi saadaan kunta. Tämä tarkoittaa
sitä, että 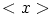 on maksimaalinen ihanne.
Saman olisi voinut päätellä suoraankin. Oletetaan,
että
on maksimaalinen ihanne.
Saman olisi voinut päätellä suoraankin. Oletetaan,
että 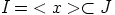 ja
ja 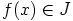 . Silloin polynomin
. Silloin polynomin 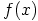 vakiotermi
vakiotermi 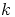 eroaa nollasta. Nyt
eroaa nollasta. Nyt 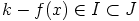 , joten
, joten 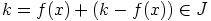 .
Edelleen
.
Edelleen 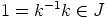 , joten
, joten 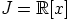 .
.
b) Olkoon 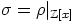 sama kuin a-kohdan kuvaus
sama kuin a-kohdan kuvaus 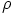 , mutta rajoitettuna
renkaaseen
, mutta rajoitettuna
renkaaseen 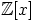 . Silloin
. Silloin 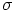 on myös homomorfismi, jonka ydin on
polynomin
on myös homomorfismi, jonka ydin on
polynomin 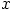 generoima ihanne. Tällä kertaa kyseinen ihanne ei kuitenkaan
ole maksimaalinen, sillä kuva
generoima ihanne. Tällä kertaa kyseinen ihanne ei kuitenkaan
ole maksimaalinen, sillä kuva 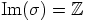 ei nyt olekaan kunta. Esimerkiksi
ei nyt olekaan kunta. Esimerkiksi
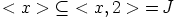 , missä ihanne
, missä ihanne 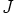 sisältää kaikki sellaiset polynomit,
joiden vakiotermi on parillinen.
sisältää kaikki sellaiset polynomit,
joiden vakiotermi on parillinen.
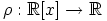 ,
, 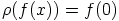 . Tämä kuvaus on selvästi
homomorfismi, koska renkaan ykkösalkio, vakiopolynomi
. Tämä kuvaus on selvästi
homomorfismi, koska renkaan ykkösalkio, vakiopolynomi 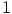 , kuvautuu
luvuksi
, kuvautuu
luvuksi 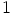 sekä kahden polynomin summan ja tulon arvot pisteessä nolla
ovat vastaavien polynomien nollapisteiden arvojen summa ja tulo.
Kuvauksen ytimen muodostavat ne polynomit, jotka saavat arvoksi nollan
pisteessä nolla. Nämä ovat täsmälleen ne polynomit, joiden vakiotermi on
nolla, eli jotka ovat jaollisia polynomilla
sekä kahden polynomin summan ja tulon arvot pisteessä nolla
ovat vastaavien polynomien nollapisteiden arvojen summa ja tulo.
Kuvauksen ytimen muodostavat ne polynomit, jotka saavat arvoksi nollan
pisteessä nolla. Nämä ovat täsmälleen ne polynomit, joiden vakiotermi on
nolla, eli jotka ovat jaollisia polynomilla 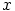 . Siis ydin on polynomin
. Siis ydin on polynomin  generoima ihanne.
Kuvaus
generoima ihanne.
Kuvaus 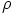 on selvästi surjektio, eli kuvaksi saadaan kunta. Tämä tarkoittaa
sitä, että
on selvästi surjektio, eli kuvaksi saadaan kunta. Tämä tarkoittaa
sitä, että 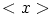 on maksimaalinen ihanne.
Saman olisi voinut päätellä suoraankin. Oletetaan,
että
on maksimaalinen ihanne.
Saman olisi voinut päätellä suoraankin. Oletetaan,
että 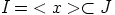 ja
ja 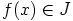 . Silloin polynomin
. Silloin polynomin 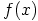 vakiotermi
vakiotermi 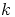 eroaa nollasta. Nyt
eroaa nollasta. Nyt 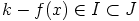 , joten
, joten 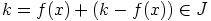 .
Edelleen
.
Edelleen 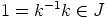 , joten
, joten 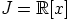 .
.
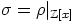 sama kuin a-kohdan kuvaus
sama kuin a-kohdan kuvaus 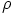 , mutta rajoitettuna
renkaaseen
, mutta rajoitettuna
renkaaseen 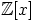 . Silloin
. Silloin 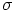 on myös homomorfismi, jonka ydin on
polynomin
on myös homomorfismi, jonka ydin on
polynomin 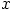 generoima ihanne. Tällä kertaa kyseinen ihanne ei kuitenkaan
ole maksimaalinen, sillä kuva
generoima ihanne. Tällä kertaa kyseinen ihanne ei kuitenkaan
ole maksimaalinen, sillä kuva 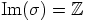 ei nyt olekaan kunta. Esimerkiksi
ei nyt olekaan kunta. Esimerkiksi
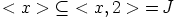 , missä ihanne
, missä ihanne 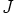 sisältää kaikki sellaiset polynomit,
joiden vakiotermi on parillinen.
sisältää kaikki sellaiset polynomit,
joiden vakiotermi on parillinen.