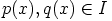 ja
ja 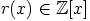 on valittu
mielivaltaisesti. Silloin
on valittu
mielivaltaisesti. Silloin 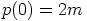 ja
ja 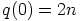 , joillakin kokonaisluvuilla
, joillakin kokonaisluvuilla 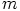 ja
ja
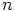 . Tästä seuraa, että
. Tästä seuraa, että
Ratkaisu:
a) Oletetaan, että polynomit 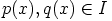 ja
ja 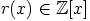 on valittu
mielivaltaisesti. Silloin
on valittu
mielivaltaisesti. Silloin 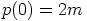 ja
ja 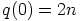 , joillakin kokonaisluvuilla
, joillakin kokonaisluvuilla 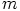 ja
ja
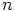 . Tästä seuraa, että
. Tästä seuraa, että
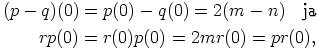
eli 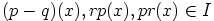 . Selvästi
. Selvästi 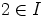 , joten
, joten 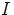 ei ole tyhjä. Siispä
ihannekriteerin mukaan
ei ole tyhjä. Siispä
ihannekriteerin mukaan 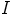 on ihanne.
on ihanne.
b) Näytetään ensin, että 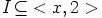 . Oletetaan siis, että
. Oletetaan siis, että 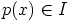 .
Silloin
.
Silloin
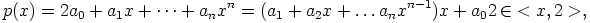 |
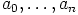 .
Näytetään toiseksi, että
.
Näytetään toiseksi, että 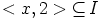 . Oletetaan, että
. Oletetaan, että 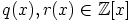 ja
ja
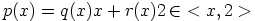 . Silloin
. Silloin 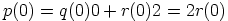 on
parillinen luku, eli
on
parillinen luku, eli 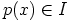 . Siispä
. Siispä 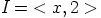 .
.
c) Näytetään, ettei 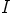 ole pääihanne. Tehdään sellainen vastaoletus, että
ole pääihanne. Tehdään sellainen vastaoletus, että
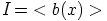 . Nyt
. Nyt
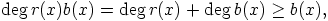 |
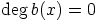 , eli
, eli 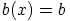 on vakiopolynomi, koska vakiopolynomi
on vakiopolynomi, koska vakiopolynomi 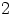 kuluu ihanteeseen
kuluu ihanteeseen 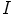 .
Toisaalta myös polynomi
.
Toisaalta myös polynomi 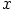 kuuluu ihanteeseen
kuuluu ihanteeseen 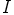 , eli on olemassa polynomi
, eli on olemassa polynomi
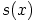 , jolla
, jolla 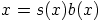 . Tällöin polynomin
. Tällöin polynomin 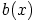 johtavan kertoimen
johtavan kertoimen 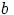 itseisarvon on oltava yksi. Siispä
itseisarvon on oltava yksi. Siispä 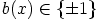 . Mutta silloin myös vakiopolynomi
. Mutta silloin myös vakiopolynomi
 kuuluu ihanteeseen
kuuluu ihanteeseen 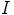 , mikä on ristiriita. Siispä
, mikä on ristiriita. Siispä 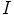 ei ole pääihanne, eikä
ei ole pääihanne, eikä
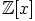 pääihannerengas.
pääihannerengas.