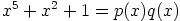 , missä
, missä
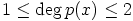 . Ensimmäisen asteen tekijöitä ei polynomilla ole, koska sillä ei
ole nollakohtia kunnassa
. Ensimmäisen asteen tekijöitä ei polynomilla ole, koska sillä ei
ole nollakohtia kunnassa 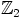 . Niinpä polynomin
. Niinpä polynomin 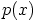 aste on kaksi. Molempien
polynomien
aste on kaksi. Molempien
polynomien 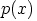 ja
ja 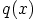 vakiokertoimien täytyy olla yksi, koska polynomin
vakiokertoimien täytyy olla yksi, koska polynomin
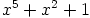 vakiokerroinkin on yksi. Saadaan
vakiokerroinkin on yksi. Saadaan
Ratkaisu:
a) Tehdään sellainen vastaoletus, että 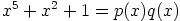 , missä
, missä
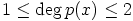 . Ensimmäisen asteen tekijöitä ei polynomilla ole, koska sillä ei
ole nollakohtia kunnassa
. Ensimmäisen asteen tekijöitä ei polynomilla ole, koska sillä ei
ole nollakohtia kunnassa 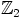 . Niinpä polynomin
. Niinpä polynomin 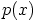 aste on kaksi. Molempien
polynomien
aste on kaksi. Molempien
polynomien 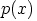 ja
ja 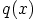 vakiokertoimien täytyy olla yksi, koska polynomin
vakiokertoimien täytyy olla yksi, koska polynomin
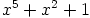 vakiokerroinkin on yksi. Saadaan
vakiokerroinkin on yksi. Saadaan
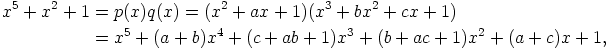
joillakin alkioilla 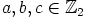 . Vertaamalla termien kertoimia saadaan neljän
yhtälön yhtälöryhmä
. Vertaamalla termien kertoimia saadaan neljän
yhtälön yhtälöryhmä
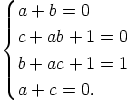 |
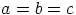 . Silloin toinen yhtälö
johtaa umpikujaan, koska sen vasemmaksi puoleksi kunnassa
. Silloin toinen yhtälö
johtaa umpikujaan, koska sen vasemmaksi puoleksi kunnassa 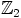 saadaan
aina
saadaan
aina
 |
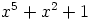 täytyy olla jaoton.
täytyy olla jaoton.
b) Suoraan laskemalla saadaan
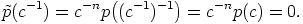 |
c) Oletetaan, että 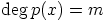 ja
ja 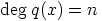 , joillakin ei-negatiivisilla
kokonaisluvuilla
, joillakin ei-negatiivisilla
kokonaisluvuilla 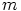 ja
ja 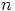 . Silloin
. Silloin 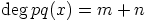 ja
ja
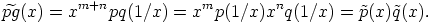 |
d) Tehdään vastaoletus, että 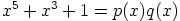 , joillakin
positiiviasteisilla polynomeilla
, joillakin
positiiviasteisilla polynomeilla 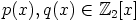 . Polynomi
. Polynomi 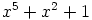 on polynomin
on polynomin 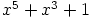 resiprookkipolynomi, joten c-kohdan mukaan
polynomi
resiprookkipolynomi, joten c-kohdan mukaan
polynomi 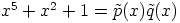 ei olisikaan jaoton. Tämä on kuitenkin
ristiriidassa a-kohdan kanssa.
ei olisikaan jaoton. Tämä on kuitenkin
ristiriidassa a-kohdan kanssa.