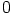 ja
ja 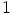 eivät kumpikaan ole polynomin
eivät kumpikaan ole polynomin 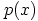 nollakohtia, eli sillä ei ole
nollakohtia kunnassa
nollakohtia, eli sillä ei ole
nollakohtia kunnassa 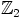 . Niinpä sillä ei ole ensimmäisen eikä kolmannen asteen
polynomitekijää. Se voisi kuitenkin jakaantua kahdeksi toisen asteen polynomiksi
. Niinpä sillä ei ole ensimmäisen eikä kolmannen asteen
polynomitekijää. Se voisi kuitenkin jakaantua kahdeksi toisen asteen polynomiksi
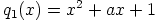 ja
ja 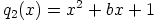 , jolloin
, jolloin
Ratkaisu:
a) 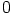 ja
ja 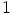 eivät kumpikaan ole polynomin
eivät kumpikaan ole polynomin 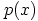 nollakohtia, eli sillä ei ole
nollakohtia kunnassa
nollakohtia, eli sillä ei ole
nollakohtia kunnassa 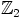 . Niinpä sillä ei ole ensimmäisen eikä kolmannen asteen
polynomitekijää. Se voisi kuitenkin jakaantua kahdeksi toisen asteen polynomiksi
. Niinpä sillä ei ole ensimmäisen eikä kolmannen asteen
polynomitekijää. Se voisi kuitenkin jakaantua kahdeksi toisen asteen polynomiksi
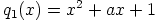 ja
ja 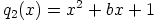 , jolloin
, jolloin
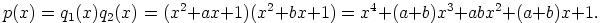 |
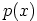 kolmannen ja ensimmäisen
asteiden termien kertoimien pitäisi olla yhtäsuuret, mikä ei pidä paikkaansa.
Niinpä polynomin
kolmannen ja ensimmäisen
asteiden termien kertoimien pitäisi olla yhtäsuuret, mikä ei pidä paikkaansa.
Niinpä polynomin 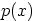 on oltava jaoton.
on oltava jaoton.
b) Koska 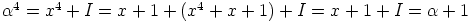 ,
on
,
on
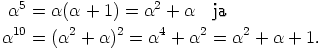
c) Huomataan, että
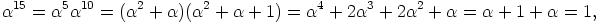 |
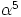 ja
ja  ovat toistensa käänteisalkioita ja
ovat toistensa käänteisalkioita ja 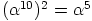 . Kunnan
. Kunnan 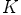 jokainen alkio on itsensä vasta-alkio, koska kunnan
jokainen alkio on itsensä vasta-alkio, koska kunnan 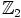 karakteristika on kaksi.
Saadaan
karakteristika on kaksi.
Saadaan 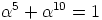 ,
, 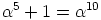 ja
ja 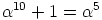 . Siispä joukko
. Siispä joukko 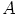 on
kunnan
on
kunnan 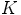 alikunta.
alikunta.