Lineaarisesti riippumattomat ja lineaarisesti riippuvat funktiot

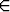
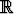1) Olkoon tutkittavana funktioiden y₁(x) = sin x, y₂(x) = cos x ja y₃(x) = cos 2x lineaarinen riippuvuus tai riippumattomuus tarkasteluvälinä koko reaaliakseli.

Testiyhtälö on

₁ sin x + ₂ cos x + ₃ cos 2x = 0  kaikilla x .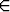

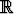Koska tämä on voimassa kaikilla arvoilla x, se on erityisesti voimassa, jos x = 0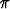, x = /2 tai x = 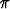. Näillä arvoilla saadaan yhtälöryhmä

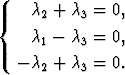
Laskemalla ensimmäinen ja kolmas yhtälö yhteen päädytään tulokseen ₃ = 0, minkä jälkeen seuraa selvästikin myös ₁ = ₂ = 0.

Koska kaikki kertoimet ₁, ₂, ₃ ovat välttämättä = 0, funktiot ovat lineaarisesti riippumattomat.

2) Olkoon tarkasteltavana funktiot y₁(x) = sin ²x, y₂(x) = cos ²x ja y₃(x) = cos 2x.

Testiyhtälö on nyt

₁ sin ²x + ₂ cos ²x + ₃ cos 2x = 0.

Samalla tavalla kuin edellä saataisiin nyt yhtälöryhmä

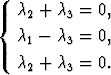
Tällä on edellisestä poiketen ratkaisuna esimerkiksi ₁ = -₂ = ₃ = 1. Tuloksesta ei kuitenkaan voida päätellä, että funktiot olisivat lineaarisesti riippuvia: voisihan olla, että valitsemalla joitakin muita arvoja kuin 0, 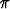/2 ja 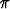muuttujalle x päädyttäisiin yhtälöryhmään, jolla nollasta eroavia ratkaisuja ei olisi. Koska kaikkia muuttujan x arvoja ei tällä tavoin voida käydä lävitse, ei menettely johda tulokseen.

Funktiot kuitenkin ovat lineaarisesti riippuvia, sillä trigonometrian kaava

cos 2x = cos ²x - sin ²x  eli   sin ²x - cos ²x + cos 2x = 0

on voimassa kaikilla muuttujan x arvoilla. Testiyhtälöllä on siten ratkaisuna ainakin ₁ = 1, ₂ = -1, ₃ = 1.