Newtonin jäähtymislaki

1600- ja 1700-lukujen vaihteessa elänyt fyysikko ja matemaatikko Isaac Newton tutki kappaleiden jäähtymistä vakiolämpöisessä ympäristössä. Kokeidensa tuloksena hän esitti ns. Newtonin jäähtymislain

.

Tässä T( t ) ilmaisee tarkasteltavan kappaleen lämpötilan hetkellä t , on ympäristön lämpötila ja k jäähtymisvakio. Käyttäen tätä yksinkertaista jäähtymislakia ratkaisemme seuraavan jäähtymisongelman.

Kuparipallo, jonka lämpötila on 100°C, upotetaan veteen, jonka lämpötilaa ylläpidetään 30°C:ssa. Upotus tapahtuu ajanhetkellä t = 0, ja kolmen minuutin päästä pallon lämpötila on pudonnut 70°C:een. Kauanko kestää ennen kuin pallon lämpötila on alle 31°C?

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

> restart;

Määritellään yhtälö lämpötilan kehitykselle.

> yht:= diff(T(t), t)=-k*(T(t)-T0);

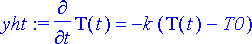
Probleeman tuntematon funktio on lämpötila T( t ).

> tuntematon:= T(t);

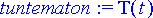
Alkuehtona on kuparipallon lämpötila on 100°C upotuksen tapahtuessa:

> alkuehto:= T(0)=100;

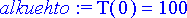
Ratkaistaan differentiaaliyhtälöryhmä ja manipuloidaan tulos käyttökelpoiseen muotoon.

> rtk:= dsolve({yht, alkuehto}, tuntematon);

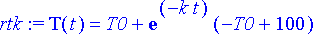
> lampo:= rhs(rtk);

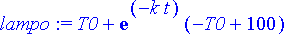
Asetetaan vakio .

> T0:= 30;

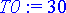
Ratkaistaan k sijoittamalla t = 180 s, jolloin kuulan läpötilan tulee olla 70°C.

> krtk:= solve(subs(t=180, lampo)=70, k);

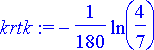
Seuraavaksi ratkaistaan, millä arvolla t lämpötila on 31°C.

> solve(subs(k=krtk, lampo)=31, t):
evalf(%);

Tämä on lähes 23 minuuttia (1380 s).

Piirretään vielä lopuksi kuvaaja, jossa näemme lämpötilan kehityksen ajan funktiona.

> plot(subs(k=krtk, lampo), t=0..1400);

On syytä huomata, että Newtonin tekemä malli on hyvin rajoitettu. Sitä käytettäessä ei kiinnitetä minkäänlaista huomiota siihen, että massiivisen kuulan ollessa kysymyksessä kuulan pinta jäähtyy sisäosaa nopeammin. Samaten kuulan ympärillä olevalle vedelle täytyy järjestää tasainen ja hyvä sekoittuminen, joka varmistaa sen tasalämpöisyyden. Kuitenkin pienille ja hyvin lämpöä johtaville kappaleille Newtonin malli on hyvä approksimaatio.

Tehtävä

Sama kuparipallo otetaan vedestä ja jäähdytetään 0°C:een. Laske Newtonin mallia käyttäen kauanko kestää, että kuparipallo lämpenee 29°C lämpötilaan, kun se jälleen upotetaan veteen.