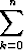 Pk(x)Dk,
Pk(x)Dk,
Jos kertalukua n oleva differentiaaliyhtälö on muotoa
Pn (x)y(n) + Pn-1(x)y(n-1) + . . . + P1(x)y' + P0(x)y = R(x),
sitä kutsutaan lineaariseksi differentiaaliyhtälöksi. Yhtälön vasempana puolena on derivaattojen lineaariyhdistely kertoimina muuttujan x funktiot Pk(x).
Jos yhtälö jaetaan korkeimman kertaluvun derivaatan kertoimella Pn(x), se saadaan normaalimuotoon. Lineaarisia differentiaaliyhtälöitä käsitellään usein tässä muodossa.
Jos R(x) = 0 kaikilla muuttujan x arvoilla, yhtälö on homogeeninen. Jos näin ei ole, se on epähomogeeninen.
Esimerkiksi ensimmäisen kertaluvun lineaarinen ja epähomogeeninen differentiaaliyhtälö on muotoa P1 (x)y' + P0(x)y = R(x), kolmannen kertaluvun normaalimuotoon saatettu homogeeniyhtälö on y''' + P2(x)y'' + P1(x)y' + P0(x)y = 0.
Lineaarinen differentiaaliyhtälö voidaan esittää lyhyemmin ottamalla käyttöön differentiaalioperaattori
L = 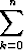 Pk(x)Dk,
Pk(x)Dk,
missä D on tavallinen derivointioperaattori ja sen potenssit tarkoittavat derivointia useampaan kertaan: esimerkiksi Dy = y', D3y = y'''. Operaattorin nollas potenssi on identiteettioperaattori, ts. sillä operointi ei vaikuta mitään: D0y = y. Operaattoria L käyttäen lineaarinen differentiaaliyhtälö saa yksinkertaisen muodon
Ly = R.
Operaattori L on ns. lineaarikuvaus, ts. sillä on ominaisuudet
L(y1 + y2) = Ly1 + Ly2, L(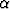 y) =
y) = 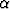 Ly,
Ly,
missä y, y1 ja y2 ovat mitä tahansa riittävän monta kertaa derivoituvia funktioita ja 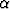 on
vakio. Ominaisuudet ovat perusteltavissa derivoinnin alkeisominaisuuksilla: summa
derivoidaan termeittäin, funktion vakiolla kertomisen ja derivoinnin järjestyksen saa
vaihtaa.
on
vakio. Ominaisuudet ovat perusteltavissa derivoinnin alkeisominaisuuksilla: summa
derivoidaan termeittäin, funktion vakiolla kertomisen ja derivoinnin järjestyksen saa
vaihtaa.