 kuvaajat
kuvaajatTarkastelun kohteena olkoon kompleksimuuttujan kompleksiarvoinen funktio
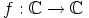 ,
,
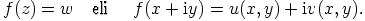
Tätä voidaan ajatella myös funktiona 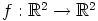 ,
,
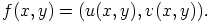
Funktiota 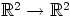 voidaan havainnollistaa asettamalla lähtötasoon
voidaan havainnollistaa asettamalla lähtötasoon
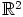 esimerkiksi
suorakulmainen tai napakoordinaattien mukainen ruudukko ja piirtämällä tämän kuva
maalitasossa
esimerkiksi
suorakulmainen tai napakoordinaattien mukainen ruudukko ja piirtämällä tämän kuva
maalitasossa 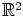 .
Esimerkiksi sinifunktion
.
Esimerkiksi sinifunktion
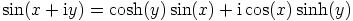
tapauksessa saadaan tällöin seuraava kuvio (joka on laadittu Mathematican Graphics‘ComplexMap‘-paketilla):
 |

|  |
Toinen vaihtoehto havainnollistamiseen on funktion
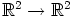 kuvaajan muodostaminen. Tämä on neliulotteisen uvxy-avaruuden kaksiulotteinen
monisto (pinta), johon kuuluvat pisteet
kuvaajan muodostaminen. Tämä on neliulotteisen uvxy-avaruuden kaksiulotteinen
monisto (pinta), johon kuuluvat pisteet
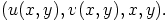
Tässä 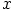 ja
ja
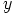 ovat pintaparametrit ja ne saavat sellaiset arvot, että piste
ovat pintaparametrit ja ne saavat sellaiset arvot, että piste
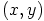 on funktion määrittelyjoukossa.
Koordinaatit
on funktion määrittelyjoukossa.
Koordinaatit 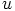 ,
,
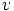 ,
,
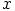 ja
ja
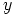 voisivat olla muussakin järjestyksessä, mutta seuraavan esityksen kannalta ylläoleva on
luontevin.
voisivat olla muussakin järjestyksessä, mutta seuraavan esityksen kannalta ylläoleva on
luontevin.
Neliulotteisen avaruuden pinnasta ei suoranaisesti voida piirtää kuvaa, mutta pudottamalla joko x- tai y-koordinaatti pois saadaan kolmiulotteisen avaruuden pinta parametrimuodossa:
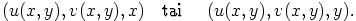
Tämän kuva voidaan piirtää tavalliseen tapaan (esimerkiksi Mathematican ParametricPlot3D-komennolla). Sinifunktion tapauksessa kuvat näyttävät seuraavilta:
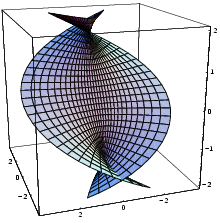

Kuvat voidaan ymmärtää kahdella tavalla:
Kyseessä on edellisessä havainnollistuksessa muodostettu uv-tason verkko nostettuna ylös uv-tasosta. Ylösnoston määrä kussakin pisteessä riippuu pisteeseen liittyvästä x-, vastaavasti y-arvosta.
Toinen tulkinta perustuu neliulotteisessa avaruudessa olevan kuvaajan projisiointiin yhdensuuntaisprojektiolla. Projektiosäde on tällöin y-, vastaavasti x-akselin suuntainen, ja kuva syntyy kolmiulotteiseen uvx- tai uvy-avaruuteen. Tilanne on analoginen kolmiulotteisessa xyz-avaruudessa olevan kohteen projisioinnille zx- tai zy-kordinaattitasoon.
Laajentamalla parametrien vaihtelualuetta saadaan myös laajemmat kuvaajat:
 | 
|
Kumpikin on siis saman neliulotteisen moniston projektiokuva. Edellisessä pinnan osat eivät osu päällekkäin, jälkimäisessä pinta peittää itseään moneen kertaan.
Edellistä kuvaa kutsutaan usein sinifunktion Riemannin pinnaksi ja sitä käytetään kompleksisen sinifunktion havainnollistamiseen. Pinnan päällekkäiset osat ovat Riemannin pinnan lehtiä. Jälkimmäinen kuva ei havainnollistamiseen kelpaa, koska eri lehdet osuvat päällekkäin.
Kolmiulotteisen avaruuden yhdensuuntaisprojektion määrittää kiinteä
taso, kuvataso, ja kiinteä suunta, projektiosäteen suunta. Kuvatason
voidaan rajoituksetta olettaa kulkevan origon kautta. Annetun pisteen
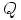 kuvapiste
kuvapiste
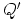 löydetään asettamalla projektiosäde pisteen kautta ja määrittämällä tämän
leikkauspiste kuvatason kanssa. Projektiosäde ei luonnollisestikaan saa olla kuvatason
suuntainen, mutta muutoin sen suunta voi olla mikä tahansa. Tärkeä erikoistapaus on
kuitenkin ortogonaaliprojektio, jossa projektiosäde on kohtisuorassa kuvatasoa
vastaan.
löydetään asettamalla projektiosäde pisteen kautta ja määrittämällä tämän
leikkauspiste kuvatason kanssa. Projektiosäde ei luonnollisestikaan saa olla kuvatason
suuntainen, mutta muutoin sen suunta voi olla mikä tahansa. Tärkeä erikoistapaus on
kuitenkin ortogonaaliprojektio, jossa projektiosäde on kohtisuorassa kuvatasoa
vastaan.
Laajempi kohde projisioidaan etsimällä periaatteessa jokaiselle sen pisteelle kuvapiste.
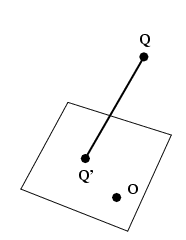
Ortogonaalisella yhdensuuntaisprojektiolla muodostettu kuva vastaa näkymää, jonka projektiosäteen suunnassa oleva katsoja kohteesta näkee.
Ajatus voidaan yleistää neliulotteiseen avaruuteen. Tällöin ortogonaalisella yhdensuuntaisprojektiolla muodostetaan kohteesta kuva kolmiulotteiseen aliavaruuteen, joka vastaa tavallisen yhdensuuntaisprojektion kuvatasoa. Kuva on kolmiulotteinen ja se voidaan ajatella neliulotteisen avaruuden asukkaan näkymäksi kohteeseen. (Kolmiulotteista kuvaa katsotaan kaksiulotteisella tietokoneen ruudulla tai paperilla, jolloin on tarvittu vielä toinen projektiokuvaus.)
Edellä esitetyt kaksi projektiota sinifunktion kuvaajasta ovat siten kaksi neliulotteisen avaruuden näkymää kuvaajaan. Yhdensuuntaisprojektiot voivat kuitenkin olla muunkinlaisia. Muuttamalla projektiosäteen suuntaa voidaan muodostaa animaatioita, joissa kohdetta katsellaan eri suunnista neliulotteisessa avaruudessa.
Seuraavat esimerkit ovat tällaisia animaatioita. Projektiosäteen suunta on määritetty neliulotteisen avaruuden pallokoordinaattien avulla:
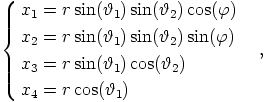
missä  ,
,
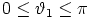 ,
,
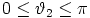 ,
,
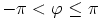 .
.
Esimerkeissä olevat janat ovat säätimiä, joissa olevaa punaista
pistettä siirtämällä voidaan muuttaa projektiosäteen suuntakulmien
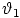 ,
,
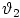 ja
ja
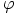 arvoja. Tällöin kohteen kuva muuntuu neliulotteisen avaruuden katselusuuntaa
vastaavasti. Tarttumalla hiirellä projektiokuvaan (joka siis on kolmiulotteisen avaruuden
olio) voidaan lisäksi kiertää kuvaa kolmiulotteisessa avaruudessa.
arvoja. Tällöin kohteen kuva muuntuu neliulotteisen avaruuden katselusuuntaa
vastaavasti. Tarttumalla hiirellä projektiokuvaan (joka siis on kolmiulotteisen avaruuden
olio) voidaan lisäksi kiertää kuvaa kolmiulotteisessa avaruudessa.
Esimerkit
∙ funktio 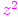
∙ funktio 
∙ funktio 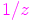
∙ eksponenttifunktio
∙ sinifunktio
∙ tangenttifunktio
∙ logaritmifunktio
∙ funktio 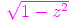
∙ funktio 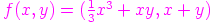
Esimerkeissä on näkyvissä myös neliulotteisen avaruuden koordinaattiakseliston kuva. Tämäkin nähdään eri suunnista, kun katselusuuntaa vaihdetaan. Värien merkitys on seuraava: u-akseli — punainen, v-akseli — vihreä, x-akseli — sininen, y-akseli — keltainen.
Esimerkit on laadittu Mathematicaa käyttäen. Apuna on ollut itse tehty lisäpaketti R2R2tools.m, jota käyttäen projisionti on laskettu; esimerkkinä sinifunktion laskemisessa käytetty Mathematican muistikirja. Animaatiot on tehty Martin Krausin LiveGraphics3D -pakettia käyttäen.
Kolmiulotteisia projektiokuvia voidaan muodostaa muistakin
neliulotteisen avaruuden kaksiulotteisista monistoista kuin funktioiden
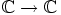 tai
tai
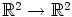 kuvaajista.
kuvaajista.
Kleinin pullo voidaan upottaa neliulotteiseen avaruuteen, ilman että se leikkaa itseään. Parametriesitykseksi voidaan tällöin valita esimerkiksi
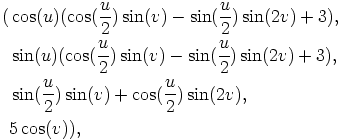
missä 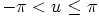 ja
ja
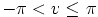 .
Muunneltavia yhdensuuntaisprojektiokuvia voidaan tällöin muodostaa täsmälleen samoin
kuin edellä. Näihin voidaan lisätä vielä neljäskin säätö: antamalla parametrile
.
Muunneltavia yhdensuuntaisprojektiokuvia voidaan tällöin muodostaa täsmälleen samoin
kuin edellä. Näihin voidaan lisätä vielä neljäskin säätö: antamalla parametrile
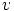 arvot
väliltä
arvot
väliltä ![$[-a,a]$](images/r2r2artikkeli48x.png) ,
missä
,
missä 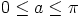 ,
saadaan Kleinin pullo avatuksi yhtä meridiaanikäyrää pitkin. Tällöin animaatio näyttää,
että Möbiuksen nauha muuttuu Kleinin pulloksi, kun nauhan vastakkaisilla puolilla olevat
pisteet liitetään yhteen.
,
saadaan Kleinin pullo avatuksi yhtä meridiaanikäyrää pitkin. Tällöin animaatio näyttää,
että Möbiuksen nauha muuttuu Kleinin pulloksi, kun nauhan vastakkaisilla puolilla olevat
pisteet liitetään yhteen.
Toisena esimerkkinä on ns. ’Flat torus’, monisto
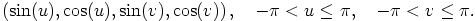
Myös tässä voidaan pinta avata neljännellä säädöllä:
![$v \in [-a,a]$](images/r2r2artikkeli51x.png) ,
,
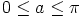 .
.
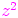 Riemannin pinnalla sijaitsee jossakin kohdassa reaalisen funktion kuvaaja, ts.
paraabeli
Riemannin pinnalla sijaitsee jossakin kohdassa reaalisen funktion kuvaaja, ts.
paraabeli  .
Missä kohdassa?
.
Missä kohdassa?
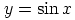 .
Missä kohdassa?
.
Missä kohdassa?
Artikkeli on suomennos esitelmästä, joka on pidetty International Mathematica Symposiumissa Avignonissa kesäkuussa 2006.