ckunta.nb

Kompleksilukujen kunnan konstruointi

Seuraava esitys osoittaa, miten kompleksilukujoukko voidaan määritellä tunnetuista reaalisista käsitteistä lähtien. Määrittelyjen jälkeen on helppoa osoittaa Mathematican laskentamahdollisuuksia käyttäen, että tulos on algebralliselta rakenteeltaan kunta.

Laskutoimistusten määrittely joukkoon

Lähtökohtana on xy-taso, ts. joukko , jonka alkioiden välille määritellään yhteen- ja kertolasku. Alkiot ovat lukupareja, Mathematican terminologialla kaksialkioisia listoja. Määrittelyä varten muodostetaan aluksi testi, joka tarkistaa, että funkion argumentit ovat sallittua tyyppiä:

In[1]:=

Laskutoimitukset ovat kahden argumentin funktioita, joiden arvona on argumenttien summa ja tulo siten kuin ne kompleksiluvuille määritellään:

In[2]:=

$summa[z_ ? ctest, w_ ? ctest] := {z_〚1〛 + w_〚1〛, z_〚2〛 + w_〚2〛}$

In[3]:=

$tulo[z_ ? ctest, w_ ? ctest] := {z_〚1〛 w_〚1〛 - z_〚2ӏ ... 14;2〛, z_〚1〛 w_〚2〛 + z_〚2〛 w_〚1〛}$

Merkintä viittaa listan z k:nteen alkioon.

Jotta päästään luonnollisempiin summan ja tulon merkintöihin, asetetaan Mathematicassa valmiiksi määritelty (mutta merkitystä vailla oleva) funktio CirclePlus tarkoittamaan funktiota summa, vastaavasti CircleTimes tarkoittamaan funktiota tulo. Tällöin laskutoimitusten symboleina voidaan käyttää renkaan sisässä olevia plus- ja kertomerkkejä (vinoristiä).

In[4]:=

In[5]:=

Tämän jälkeen laskutoimitukset toimivat normaaliin tapaan:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Nolla, ykkönen ja imaginaariyksikkö ovat erikoisasemassa olevia kompleksilukuja ja näille annetaan omat nimet:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Tälöin pätee

In[11]:=

Out[11]=

Tuloksena on saatu yhteen- ja kertolaskulla varustettu kompleksilukujen joukko C.

Kuntastruktuuri

Joukko C voidaan osoittaa kunnaksi tarkistamalla kunta-aksioomien voimassaolo. Näissä esiintyy kolme mielivaltaisesti valittua kompleksilukua, joten luodaan kolme symbolista kaksialkioista listaa:

In[12]:=

$a = {α_1, α_2} ; b = {β_1, β_2} ; c = {γ_1, γ_2} ;$

Näitä käyttäen tarkistetaan kunta-aksioomien voimassaolo yksi kerrallaan.

Yhteenlaskun vaihdannaisuus:

In[13]:=

Out[13]=

Yhteenlaskun liitännäisyys:

In[14]:=

Out[14]=

Yhteenlaskun neutraalialkio on nolla-alkio o:

In[15]:=

Out[15]=

Alkion a={,} vasta-alkio löydetään ratkaisemalla yhtälö:

In[16]:=

$x = {ξ_1, ξ_2} ;$

In[17]:=

Out[17]=

${{ξ_1 -α_1, ξ_2 -α_2}}$

In[18]:=

Out[18]=

${-α_1, -α_2}$

Kertolaskun vaihdannaisuus:

In[19]:=

Out[19]=

Kertolaskun liitännäisyys, missä tarvitaan eksplisiittinen sievennyskäsky:

In[20]:=

Out[20]=

${(α_1 β_1 - α_2 β_2) γ_1 - (α_2 β_1 + α_1 β_2) ... 5;_1 (β_2 γ_1 + β_1 γ_2) + α_2 (β_1 γ_1 - β_2 γ_2)}$

In[21]:=

Out[21]=

Kertolaskun neutraalialkio on ykkösalkio e:

In[22]:=

Out[22]=

Alkion a={,} käänteisalkio löydetään ratkaisemalla yhtälö:

In[23]:=

Out[23]=

${{ξ_1α_1/(α_1^2 + α_2^2), ξ_2 -α_2/(α_1^2 + α_2^2)}}$

In[24]:=

Out[24]=

${α_1/(α_1^2 + α_2^2), -α_2/(α_1^2 + α_2^2)}$

Osittelulaki:

In[25]:=

Out[25]=

${α_1 (β_1 + γ_1) - α_2 (β_2 + γ_2), α_2 (β_1 + γ ... #945;_2 γ_2, α_2 β_1 + α_1 β_2 + α_2 γ_1 + α_1 γ_2}$

In[26]:=

Out[26]=

Koska kaikki kunta-aksioomat ovat voimassa, joukko C varustettuna edellä määritellyillä laskutoimituksilla on todellakin kunta.

Lisäyksiä laskutoimitusten määrittelyyn

Koska sekä summa että tulo ovat liitännäisiä, olisi luontevaa sallia sulkujen poisjättäminen useamman termin summassa ja useamman tekijän tulossa. Ilman lisämäärittelyjä tämä ei kuitenkaan onnistu, koska funktiot summa ja tulo on edellä määritelty vain kahden argumentin tapauksessa.

In[27]:=

Out[27]=

$summa[{α_1, α_2}, {β_1, β_2}, {γ_1, γ_2}]$

Tarvittavat lisämäärittelyt ovat seuraavat:

In[28]:=

In[29]:=

In[30]:=

In[31]:=

Tämän jälkeen sulkujen poisjättäminen tai mielivaltainen ryhmittely toimii:

In[32]:=

Out[32]=

${α_1 + β_1 + γ_1, α_2 + β_2 + γ_2}$

In[33]:=

Out[33]=

${3 α_1 + 2 β_1 + 2 γ_1, 3 α_2 + 2 β_2 + 2 γ_2}$

In[34]:=

Out[34]=

${-2 α_1 α_2^2 + α_1 (α_1^2 - α_2^2), 2 α_1^2 α_2 + α_2 (α_1^2 - α_2^2)}$

In[35]:=

Out[35]=

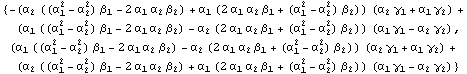
${-(α_2 ((α_1^2 - α_2^2) β_1 - 2 α_1 α_2 β_2) + α_1 ( ... #945;_2 β_1 + (α_1^2 - α_2^2) β_2)) (α_1 γ_1 - α_2 γ_2)}$

In[36]:=

Out[36]=

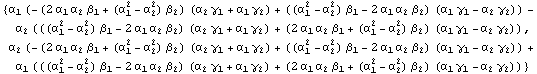
${α_1 (-(2 α_1 α_2 β_1 + (α_1^2 - α_2^2) β_2) (α_2 &# ... #945;_2 β_1 + (α_1^2 - α_2^2) β_2) (α_1 γ_1 - α_2 γ_2))}$

In[37]:=

Out[37]=

Summan ja tulon laskujärjestystä ei tarvitse erikseen määritellä, sillä Mathematicassa on valmiina määrittely, jonka mukaan ⊗ lasketaan ensin ja ⊕ sen jälkeen:

In[38]:=

Out[38]=

Myös ei-negatiivinen kokonaislukupotenssi voidaan määritellä:

In[39]:=

In[40]:=

Huomaa, että symbolina ei ole tavallinen hattumerkki,vaan pieni vinoneliö!

In[41]:=

Out[41]=

${α_1^2 - α_2^2, 2 α_1 α_2}$

In[42]:=

Out[42]=

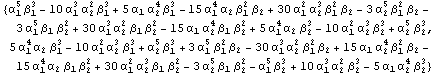
${α_1^5 β_1^3 - 10 α_1^3 α_2^2 β_1^3 + 5 α_1 α_2^4 β_ ... α_1^5 β_2^3 + 10 α_1^3 α_2^2 β_2^3 - 5 α_1 α_2^4 β_2^3}$

In[43]:=

Out[43]=

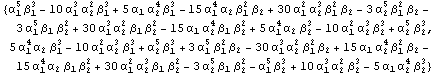
${α_1^5 β_1^3 - 10 α_1^3 α_2^2 β_1^3 + 5 α_1 α_2^4 β_ ... α_1^5 β_2^3 + 10 α_1^3 α_2^2 β_2^3 - 5 α_1 α_2^4 β_2^3}$

In[44]:=

Out[44]=

Siirtyminen kompleksilukujen tavanomaiseen esitykseen

Edellä on rakennettu kompleksilukuaritmetiikkaa Mathematicaan tarkoituksena osoittaa, miten tämä määritelmien pohjalta tulisi periaatteessa tehdä. Lopuksi on syytä katsoa, miten voidaan siirtyä kompleksilukujen tavanomaiseen esitykseen, mikä toki on Mathematicassa valmiinakin. Edellä käsitellyt kaksialkioisen listan muotoiset kompleksiluvut voidaan muuntaa normaaliin muotoon funktiolla

In[45]:=

Tässä i tarkoittaa imaginaariyksikköä. Esimerkiksi:

In[46]:=

Out[46]=

In[47]:=

Out[47]=

In[48]:=

Out[48]=

In[49]:=

Out[49]=

Varsinaisesti kompleksiluvuilla laskettaessa ne syötetään Mathematicassa suoraan normaalimuodossa. Laskutoimitussymbolit ovat samoja kuin reaalisten muuttujien tapauksessa. Esimerkiksi:

In[50]:=

Out[50]=

In[51]:=

Out[51]=

In[52]:=

$Table[^n, {n, 0, 10}]$

Out[52]=

Harjoitustehtäviä

1) Laske kompleksilukujen =-5+7i ja =-2-11i summa, tulo ja osamäärä sekä edellä olevan määritelmän mukaisella formalismilla että normaalia tapaa käyttäen.

2) Laske kompleksilukujen = cos()+i sin() ja = cos()+i sin() tulo ja osamäärä sekä luvun käänteisluku edellä olevan määritelmän mukaisesti. Sievennä tulokset.

3) Määrittele funktiot, jotka antavat reaalilukuparina esitetyn kompleksiluvun liittoluvun ja itseisarvon. Tarkista näitä käyttäen, että seuraavat yhtälöt ovat voimassa kaikille kompleksiluvuille: a) =+, b) = , c) =z, d) ||=|z|, e) z =|z, f) | |=||||.

Simo K. Kivelä 23.4.2005

Created by Mathematica (September 22, 2005)