12 Lisää määrätystä integraalista
12.1 Integraalin arvioimisesta
Tehtävä 521
Osoita:
1 < 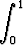
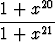 dx <
dx < 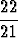 .
.
Tehtävä 522
Osoita:
0 < 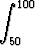
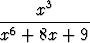 dx < 15 . 10-5.
dx < 15 . 10-5.
Tehtävä 523
Osoita:
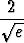 <
< 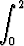 ex2-x dx < 2e2.
ex2-x dx < 2e2.
Tehtävä 524
Olkoon k > 0. Osoita:
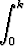
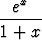 dx > k.
dx > k.
Tehtävä 525
Olkoon a > e. Osoita:
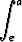
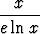 dx > a - e.
dx > a - e.
Tehtävä 526
Osoita, että
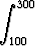
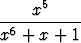 dx = ln 3 -
dx = ln 3 - 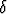 ,
,
missä 10-12 < 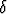 < 10-10.
< 10-10.
Tehtävä 527
Funktiosta f oletetaan, että f(0) = 1, sen derivaatta f' on jatkuva ja 1 + x < f' (x) < ex välillä [-1, 0]. Mitä arvoja f(-1) voi saada?Tehtävä 528
Olkoon funktio f jatkuva välillä [a, b] ja olkoon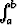 f(x)h(x) dx = 0, olipa
h mikä tahansa integroituva funktio. Osoita, että f(x) = 0 kaikilla x
f(x)h(x) dx = 0, olipa
h mikä tahansa integroituva funktio. Osoita, että f(x) = 0 kaikilla x 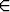 [a, b].
[a, b].
12.2 Määrätyn integraalin väliarvolause
Tehtävä 529
Määritä integraalilaskun väliarvolauseessa esiintyvä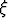 , kun kyseessä on
integraali
, kun kyseessä on
integraali
a) 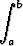 (
(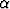 x +
x + 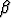 ) dx, b)
) dx, b) 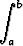 x2 dx.
x2 dx.
Tehtävä 530
Määritä raja-arvo
limx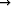 2
2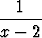
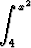 et2
dt.
et2
dt.
Tehtävä 531
Olkoon funktio f jatkuva ja funktio g määritelty seuraavasti:
g(x) = ![x/h2, kun x (- [0,h],
{
(2h - x)/h2, kun x (- [h,2h],
0 muulloin.](kuvat/ra1382x.gif)
Osoita (yleistettyä) integraalilaskun väliarvolausetta käyttäen, että
limh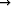 0+
0+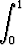 f(x)g(x) dx = f(0).
f(x)g(x) dx = f(0).
12.3 Epäoleelliset integraalit
Tehtävä 532
Laske arvo tai osoita hajaantuminen seuraaville integraaleille:a) 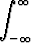 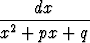 (p2 < 4q), (p2 < 4q), | b) 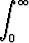 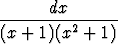 , , | c) 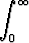 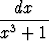 , , | |||||||||
d) 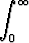 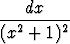 , , | e) 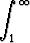 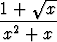 dx, dx, | f) 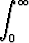 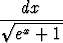 , , | |||||||||
g) 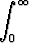 e-ax cos bx dx (a > 0), e-ax cos bx dx (a > 0), | h) 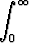 e-ax sin bx dx (a > 0), e-ax sin bx dx (a > 0), | ||||||||||
i) 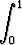 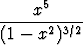 dx, dx, | j) 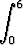 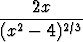 dx, dx, | k) 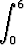 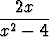 dx, dx, | |||||||||
l) 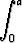 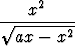 dx (a dx (a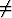 0), 0), | m) 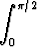 tan x dx, tan x dx, | n) 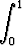 ln x dx. ln x dx. |
Tehtävä 533
Johda palautuskaava integraalille
In = 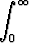 xne-x dx, n = 0, 1, 2, . . . ,
xne-x dx, n = 0, 1, 2, . . . ,
ja laske integraali sen avulla.
Tehtävä 534
Määritä a ja b siten, että integraali
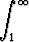
![[ ]
2x2 + bx + a
-------------- 1
x(2x + a)](kuvat/ra1415x.gif) dx
dx
suppenee ja on arvoltaan = 1.
Tehtävä 535
Tutki, millä arvoilla k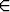
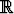 seuraavat integraalit suppenevat:
seuraavat integraalit suppenevat:
a) 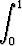
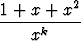 dx, b)
dx, b) 
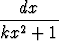 , c)
, c) 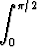 sin kx dx.
sin kx dx.
Tehtävä 536
Millä arvoilla k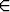
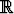 integraali
integraali
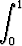
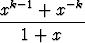 dx
dx
a) ei ole epäoleellinen, b) on epäoleellinen ja suppenee?
Tehtävä 537
Laske seuraavan epäoleellisen integraalin arvo tai osoita sen hajaantuminen:
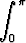
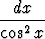 .
.
Tehtävä 538
Laske
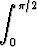
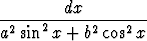 (ab
(ab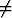 0).
0).
Tehtävä 539
Sievennä funktion
f(x) = 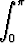
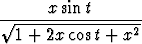 dt
dt
lauseke ja piirrä kuvaaja.
Tehtävä 540
Osoita, että on olemassa vakio M > 0 siten, että kaikilla
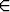 ]0, 1[
pätee
]0, 1[
pätee
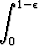
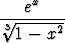 dx < M.
dx < M.
Tehtävä 541
Todista:
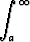 f suppenee
f suppenee 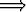 limb
limb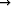
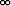
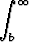 f = 0.
f = 0.
Tehtävä 542
Todista:a) 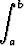 |f| suppenee |f| suppenee  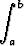 f suppenee, f suppenee, | |||
b) 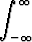 |f| suppenee |f| suppenee 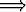 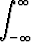 f suppenee. f suppenee. |
Tehtävä 543
Olkoon funktio f jatkuva, kun x > 1, ja
limx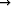
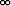
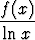 = -2.
= -2.
Osoita, että integraali 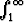 ef(x) dx suppenee.
ef(x) dx suppenee.
Tehtävä 544
Arvoilla x > 0 määritellään gammafunktio integraalilla
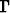 (x) =
(x) = 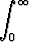 tx-1e-t dt.
tx-1e-t dt.
Päättele, että integraali suppenee, jos x > 0. Suppeneeko integraali, jos x < 0?
Tehtävä 545
Piirrä gammafunktion kuvaaja jonkin tietokoneohjelman avulla. Tarkastele erikseen positiivisia ja negatiivisia muuttujan arvoja. Tiedätkö, miten gammafunktio on määritelty negatiivisilla muuttujan arvoilla?Tehtävä 546
Laske käyrän y = xe-x2/2 ja sen asymptootin väliin jäävän rajoittamattoman tasokuvion ala.Tehtävä 547
xz-tason käyrä z = exp(-x2) pyörähtää z-akselin ympäri, jolloin syntyy xy-tason yläpuolella sijaitseva (ääreetömyyteen joka suunnassa ulottuva) pinta. Laske tämän pinnan ja xy-tason väliin jäävän alueen tilavuus, mikäli se on äärellinen.Tehtävä 548
Osoita, että avaruuskäyrän r(t) = e-t(cos t i + sin t j + k), 0 < t <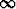 , pituus
on äärellinen ja määritä se.
, pituus
on äärellinen ja määritä se.
Tehtävä 549
Käyrä y = e-x, 0 < x <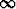 , pyörähtää x-akselin ympäri. Laske syntyvän
(äärettömyyteen ulottuvan) pyörähdyspinnan ala.
, pyörähtää x-akselin ympäri. Laske syntyvän
(äärettömyyteen ulottuvan) pyörähdyspinnan ala.
Tehtävä 550
Käyrä y = 1/x, 1 < x <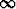 , pyörähtää x-akselin ympäri, jolloin syntyy
äärettömyyteen ulottuva suppilomainen astia. Laske tämän tilavuus. Astian
halkaisijataso on levy {(x, y) | |y| < 1/x, x > 1}. Mikä on tämän pinta-ala? Jos astia
täytetään maalilla, tuleeko halkaisijataso kokonaisuudessaan peitetyksi maalilla?
, pyörähtää x-akselin ympäri, jolloin syntyy
äärettömyyteen ulottuva suppilomainen astia. Laske tämän tilavuus. Astian
halkaisijataso on levy {(x, y) | |y| < 1/x, x > 1}. Mikä on tämän pinta-ala? Jos astia
täytetään maalilla, tuleeko halkaisijataso kokonaisuudessaan peitetyksi maalilla?
Tehtävä 551
Määritä kaarenpituus napakoordinaattikäyrälle r = e- ,
, 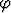
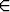 [0,
[0, 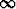 [. Laske
käyrän kaarevuus parametrin
[. Laske
käyrän kaarevuus parametrin 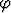 funktiona. Mikä on kaarevuussäteen raja-arvo, kun
funktiona. Mikä on kaarevuussäteen raja-arvo, kun
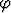
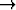
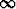 ? Piirrä käyrä.
? Piirrä käyrä.