1 Vektorimuuttujan funktiot
1.1 Avaruus  n
n
Tehtävä 1
Todista Cauchyn –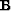
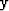








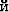 ’n – Schwarzin epäyhtälö avaruudessa
’n – Schwarzin epäyhtälö avaruudessa  n.
n.
Tehtävä 2
Tutki, onko joukko
S = 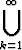 { (x, y)
{ (x, y) 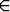
 | x
| x 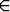 [0, 1], y =
[0, 1], y = 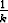 }.
}.
kompakti, ts. rajoitettu ja suljettu.
Tehtävä 3
Avaruuden n joukon kompaktisuuden määritelmänä pidettäköön sitä, että se
on suljettu ja rajoitettu; joukko olkoon suljettu, jos sen komplementti on avoin; joukko
olkoon avoin, jos sen jokainen piste on sisäpiste. Sisäpiste on piste, jolla on jokin
ympäristö, joka kokonaisuudessaan sisältyy joukkoon. Joukon kasautumispiste on piste,
jonka jokaisessa ympäristössä on muitakin joukon pisteitä kuin kasautumispiste itse (jonka
ei edes tarvitse kuulua joukkoon). Osoita, että joukko A
n joukon kompaktisuuden määritelmänä pidettäköön sitä, että se
on suljettu ja rajoitettu; joukko olkoon suljettu, jos sen komplementti on avoin; joukko
olkoon avoin, jos sen jokainen piste on sisäpiste. Sisäpiste on piste, jolla on jokin
ympäristö, joka kokonaisuudessaan sisältyy joukkoon. Joukon kasautumispiste on piste,
jonka jokaisessa ympäristössä on muitakin joukon pisteitä kuin kasautumispiste itse (jonka
ei edes tarvitse kuulua joukkoon). Osoita, että joukko A 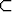
 n on kompakti, jos ja vain jos
sen jokaisella äärettömän monen alkion osajoukolla on kasautumispiste joukossa A.
n on kompakti, jos ja vain jos
sen jokaisella äärettömän monen alkion osajoukolla on kasautumispiste joukossa A.
1.2 Funktion raja-arvo ja jatkuvuus
Tehtävä 4
Todista, että seuraavilla kahden reaalimuuttujan reaaliarvoisilla funktioilla on raja-arvo origossa ja määritä tämä:
a) 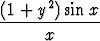 , b)
, b) 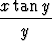 .
.
Tehtävä 5
Olkoon funktiolla f : E3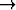 E3 raja-arvo
E3 raja-arvo
limr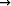 r0f(r) = a
r0f(r) = a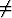 o.
o.
Todista raja-arvon määritelmään perustuen, että
limr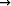 r0
r0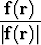 =
=  .
.
Tehtävä 6
Todista suoraan raja-arvon määritelmään perustuen, että funktio f : 2
2 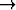
 2,
f(x, y) = (x + y, xy), on jatkuva pisteessä (1, 1).
2,
f(x, y) = (x + y, xy), on jatkuva pisteessä (1, 1).
Tehtävä 7
Funktio f : 3
3 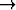
 olkoon jatkuva pisteessä (x0, y0, z0). Määritellään funktio
g :
olkoon jatkuva pisteessä (x0, y0, z0). Määritellään funktio
g :  2
2 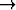
 asettamalla g(x, y) = f(x, y, z0). Todista, että g on jatkuva pisteessä
(x0 , y0 ).
asettamalla g(x, y) = f(x, y, z0). Todista, että g on jatkuva pisteessä
(x0 , y0 ).
Tehtävä 8
Määrittele tasainen jatkuvuus funktiolle f : 2
2 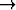
 . Tutki, ovatko funktiot
a) f(x, y) = 3x + 5y, b) f(x, y) = xy tasaisesti jatkuvia määrittelyjoukossa
. Tutki, ovatko funktiot
a) f(x, y) = 3x + 5y, b) f(x, y) = xy tasaisesti jatkuvia määrittelyjoukossa  2.
2.
1.3 Esimerkkejä vektorimuuttujan funktioista
Tehtävä 9
Millä muuttujien arvoilla seuraavat kahden muuttujan reaaliarvoiset funktiot f(x, y) ovat määriteltyjä? Piirrä näiden kuvaajat.
a) x2 - y2, b) xy - yx, c) 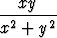 , d)
, d) 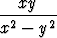 .
.
Tehtävä 10
Piirrä korkeuskäyräkuvat edellisen tehtävän funktioiden kuvaajista.Tehtävä 11
Piirrä kahden muuttujan funktionf(x, y) = xe-(x2+y2)
kuvaaja (pinta), kun -3 < x < 3, -3 < y < 3.
Tehtävä 12
Tutki funktion f(x, y) = x3 + y3 - 3xy kuvaajaa piirtämällä sen tasa-arvokäyriä f(x, y) = vakio. Mikä käyrä saadaan, jos vakio = 0?Tehtävä 13
Piirrä kuvaaja funktiolle
f(x, y) = 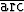 tan
tan 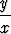 , x
, x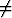 0.
0.
Mitä arvoja funktio saa origon ympäristössä? Miten funktion kuvaajan muodostamaa pintaa voisi kuvata?
Tehtävä 14
Tarkastellaan pintaa z = xy2(1 - x)y, 0 < x < 1, y > 0. Piirrä pinnan ja tasojen y = vakio leikkauskäyriä. Miten leikkauskäyrät z = fy(x) käyttäytyvät, kun y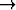
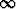 ? Onko olemassa rajafunktiota z = f(x) = limy
? Onko olemassa rajafunktiota z = f(x) = limy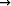
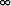 fy(x)?
fy(x)?
Tehtävä 15
Tarkastellaan kuvausta f : 2
2 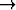
 2,
2,
f(r, 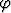 ) = (r cos
) = (r cos 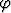 , r sin
, r sin 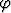 ).
).
Piirrä lähtöjoukon suorakulmainen koordinaattiruudusto ja tämän kuva maalijoukossa. Onko kuvaus bijektio?
Tehtävä 16
Funktio f : 2
2 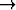
 2 määritellään asettamalla
2 määritellään asettamalla
(u, v) = f(x, y) = (ex cos y, ex sin y).
Lähtötasoa voidaan kutsua xy-tasoksi, maalitasoa uv-tasoksi. Tutki, millaiseksi uv-tason kuvioksi kuvautuu xy-tason neliö { (x, y) | 0 < x < 1, 0 < y < 1 }.
Tehtävä 17
Muodosta xy-tason suorakulmainen pistehila ja piirrä sen kuva. Kuvaa hila tämän jälkeen funktiolla f : 2
2 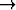
 2, f(x, y) = (ex cos y, ex sin y) ja piirrä kuvahila.
Millaisesta kuvauksesta f on kysymys?
2, f(x, y) = (ex cos y, ex sin y) ja piirrä kuvahila.
Millaisesta kuvauksesta f on kysymys?
Tehtävä 18
Olkoot f : 2
2 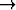
 3 ja g :
3 ja g :  2
2 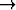
 2 kuvauksia:
2 kuvauksia:
f(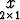 ) = Ax, A =
) = Ax, A = 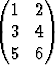 ; g(x, y) = (ex cos y, ex sin y).
; g(x, y) = (ex cos y, ex sin y).
Muodosta yhdistetyn funktion fog lauseke.
Tehtävä 19
Koko avaruuden täyttävä neste kiertää z-akselin ympäri siten, että nestehiukkasen kulmanopeus on suoraan verrannollinen sen z-koordinaatin neliöön. Muodosta vektorimuuttujan vektoriarvoinen funktio, joka esittää nestehiukkasen nopeusvektoria sen paikan funktiona. (Tällaista funktiota kutsutaan vektorikentäksi; jokaiseen avaruuden pisteeseen tai oikeammin sen paikkavektoriin r liittyy kentän vektori f(r)).Tehtävä 20
Robotin tasossa liikkuva käsivarsi muodostuu kahdesta vivusta, joista edellinen on kiinnitetty toisesta päästä origoon ja toiseen on nivelletty jälkimmäinen vipu. Vipujen pituudet ovat a ja b. Käsivartta ohjataan säätämällä edellisen vivun suuntakulmaa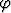 ja vipujen välistä kulmaa
ja vipujen välistä kulmaa 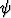 . Lausu käsivarren vapaan pään koordinaatit
(x, y) ohjauskulmien funktiona. Vastaako jokaista vapaan pään asemaa yksikäsitteiset
ohjauskulmien arvot?
. Lausu käsivarren vapaan pään koordinaatit
(x, y) ohjauskulmien funktiona. Vastaako jokaista vapaan pään asemaa yksikäsitteiset
ohjauskulmien arvot?
Tehtävä 21
Tason käänteissäteinen muunnos (inversio) on kuvaus 2
2 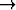
 2. Pisteen
P
2. Pisteen
P  (x, y) kuvaksi asetetaan piste P '
(x, y) kuvaksi asetetaan piste P '  (x', y') siten, että P ja P ' sijaitsevat samalla
origosta O alkavalla säteellä ja etäisyyksille pätee |OP | |OP '| = 1. Johda kuvauksen
komponenttifunktioiden lausekkeet.
(x', y') siten, että P ja P ' sijaitsevat samalla
origosta O alkavalla säteellä ja etäisyyksille pätee |OP | |OP '| = 1. Johda kuvauksen
komponenttifunktioiden lausekkeet.
Tehtävä 22
Eräässä karttaprojektiossa ajatellaan kiedottavaksi lieriö maapallon ympäri siten, että se sivuaa palloa päiväntasaajaa pitkin. Pallon pinnan piste projisioidaan lieriölle keskusprojektiolla, jonka keskus on maapallon keskipisteessä. Lopuksi lieriö leikataan auki jotakin meridiaanin kuvaa pitkin ja levitetään tasokartaksi. Johda lausekkeet sille kuvaukselle 2
2 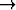
 2, joka kuvaa maantieteelliset pallokoordinaatit
suorakulmaisiksi karttakoordinaateiksi. Oletetaan, että lieriö on leikattu auki meridiaania
180o pitkin ja karttakoordinaattien origo on kartan vasemmassa laidassa keskellä. Kartan
mittakaava olkoon 1 : d päiväntasaajalla.
2, joka kuvaa maantieteelliset pallokoordinaatit
suorakulmaisiksi karttakoordinaateiksi. Oletetaan, että lieriö on leikattu auki meridiaania
180o pitkin ja karttakoordinaattien origo on kartan vasemmassa laidassa keskellä. Kartan
mittakaava olkoon 1 : d päiväntasaajalla.