12 Derivointioperaattoreista geometrisissa avaruuksissa
12.1 Gradientti, divergenssi ja roottori
Tehtävä 328
Laske . u, kun u on vektorikenttä
. u, kun u on vektorikenttä
| a) (z - y)i + (x - z)j + (y - x)k, | |||
| b) exyz(i + x ln y j + x2z k), | |||
| c) (x3z - 2xyz)i + (xy - 3x2yz)j + (yz2 - xz)k. |
Tehtävä 329
Laske × u, kun u on vektorikenttä
× u, kun u on vektorikenttä
| a) 2xyz i + x2z j + x2y k, | |||
| b) exyz(i + x ln y j + x2z k), | |||
| c) (x2 + y2 + z2)(xi + yj + zk). |
Tehtävä 330
Laske vektorikentänu(r) = (yx2 + z)i + (zy2 + x)j + (xz2 + y)k
divergenssi ja roottori. Mikä on divergenssin arvo niissä pisteissä, missä roottori on = o?
Tehtävä 331
Piirrä kuva vektorikentän u(x, y, z) = z2(x i + y j) + k ja xz-tason leikkauksesta. Millaisia symmetriaominaisuuksia kentällä on?Tehtävä 332
Laske vektorikentän u(x, y, z) = z2(x i + y j) + k vuo kuution |x| <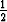 , |y| <
, |y| < 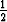 , |z| <
, |z| < 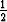 pinnan läpi. Laske myös kentän divergenssi ja roottori.
pinnan läpi. Laske myös kentän divergenssi ja roottori.
Tehtävä 333
Piirrä samaan kuvaan funktionu(x, y) = xe-x2-y2
tasa-arvokäyrät ja tämän gradientin  u(x, y) kenttävektorit. Miten tasa-arvokäyrät ja
kenttävektorit suhtautuvat toisiinsa?
u(x, y) kenttävektorit. Miten tasa-arvokäyrät ja
kenttävektorit suhtautuvat toisiinsa?
Tehtävä 334
Vektorikenttä u on riippumaton z-koordinaatista ja sen z-komponentti on = 0. xy-tasossa olevat kenttävektorit ovat origokeskisten ympyröiden (positiiviseen kiertosuuntaan osoittavia) tangenttivektoreita, joiden pituus riippuu ympyrän säteestä. Määritä kenttä, kun tiedetään, että × u = o. Piirrä kuva kentästä.
× u = o. Piirrä kuva kentästä.
12.2 Laskusääntöjä
Tehtävä 335
Osoita: a) . r0 =
. r0 = 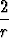 , b)
, b)  × r0 = o.
× r0 = o.
Tehtävä 336
Sievennä . (rpr). Millä luvun p arvoilla tulos on vakio?
. (rpr). Millä luvun p arvoilla tulos on vakio?
Tehtävä 337
Sievennä r . [
[ . (rpr)].
. (rpr)].
Tehtävä 338
Olkoon u(r) vektorikenttä. Saata yksinkertaisimpaan muotoonsa a) (u × ) . r, b) (u ×
) . r, b) (u ×  ) × r.
) × r.
Tehtävä 339
Olkoon e vakioyksikkövektori ja u(r) vektorikenttä. Osoita:
e . [ (e . u) +
(e . u) +  × (e × u)] =
× (e × u)] =  . u.
. u.
Tehtävä 340
Olkoot
f(r) = a . r ja g(r) = 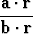
geometrisen avaruuden E3 skalaarikenttiä. Laske  f ja
f ja  g. Vektorit a ja b ovat vakioita.
g. Vektorit a ja b ovat vakioita.
Tehtävä 341
Olkoot a ja b vakiovektoreita. Laske skalaarikolmitulon [a, b, r] gradientti.Tehtävä 342
Olkoot a ja b vakiovektoreita. Osoita:
 [(r × a) . (r × b)] = b × (r × a) + a × (r × b).
[(r × a) . (r × b)] = b × (r × a) + a × (r × b).
Tehtävä 343
Olkoon c vakiovektori. Osoita vektoreita komponenteittain kirjoittamatta, että

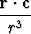 =
=  ×
× 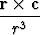 .
.
Tehtävä 344
Olkoon c vakiovektori. Sievennä × (r2c × r).
× (r2c × r).
Tehtävä 345
Olkoon c vakiovektori ja h :
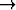
 derivoituva funktio. Määritä
skalaarikenttien F ja G lausekkeet kehitelmässä
derivoituva funktio. Määritä
skalaarikenttien F ja G lausekkeet kehitelmässä
 × (r × h(r)c) = F (r)r - G(r)c.
× (r × h(r)c) = F (r)r - G(r)c.
Tehtävä 346
Lausu funktion F derivaattojen ja paikkavektorin pituuden r avulla r . (
( 2 F (r)).
2 F (r)).
Tehtävä 347
Tutki, millä vakion p arvolla yhtälön
 2[r2F (r)] = r2
2[r2F (r)] = r2 2F (r) + p r .
2F (r) + p r .  F (r)
F (r)
ainoa ratkaisu on identtisesti häviävä funktio F (r) = 0.
Tehtävä 348
Olkoon F (r) avaruuden E3 skalaarikenttä, joka toteuttaa osittaisdifferentiaaliyhtälön
 2[(r .
2[(r .  r)F (r)] = 0.
r)F (r)] = 0.
Muodosta funktiota F koskeva tavallinen differentiaaliyhtälö ja tutki, millainen skalaarikenttä F (r) voi olla.
Tehtävä 349
Ratkaise Laplacen differentiaaliyhtälö 2u = 0 kolmiulotteisessa
avaruudessa, kun tiedetään, että u on pallosymmetrinen, ts. u(x, y, z) = F (r). Mikä on
yhtälön ratkaisu kaksiulotteisessa tasossa, kun u(x, y) = F (r)?
2u = 0 kolmiulotteisessa
avaruudessa, kun tiedetään, että u on pallosymmetrinen, ts. u(x, y, z) = F (r). Mikä on
yhtälön ratkaisu kaksiulotteisessa tasossa, kun u(x, y) = F (r)?
12.3 Käyräviivaiset koordinaatistot
Tehtävä 350
Yhtälöt
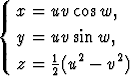
määrittävät käyräviivaiset koordinaatit u, v, w, ns. parabolisen koordinaatiston. Määritä koordinaatiston yksikkövektorit. Ovatko ne ortogonaalisia? Millaisia ovat koordinaattipinnat? Laske suure H.
Tehtävä 351
Pisteen suorakulmaiset koordinaatit ovat (3, 3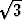 , -5/2). Laske
pisteen paraboliset koordinaatit ja lausu siihen liittyvät paraboliset yksikkövektorit
{i, j, k}-kannassa.
, -5/2). Laske
pisteen paraboliset koordinaatit ja lausu siihen liittyvät paraboliset yksikkövektorit
{i, j, k}-kannassa.
Tehtävä 352
Lausu Laplacen operaattori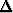 =
=  2 parabolisten koordinaatten avulla.
2 parabolisten koordinaatten avulla.
Tehtävä 353
Bipolaariset tasokoordinaatit u, v määritellään yhtälöillä
x = 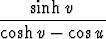 , y =
, y =  .
.
Tutki, minkälaiset ovat koordinaattikäyrät ja annettuun pisteeseen liittyvät bipolaariset yksikkövektorit. Ovatko koordinaatit suorakulmaisia?
12.4 Lieriö- ja pallokoordinaatisto
Tehtävä 354
Osoita, että lieriökoordinaateille pätee
a) 
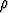 = e
= e , b)
, b) 
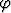 =
= 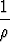 e
e , c)
, c)  z = ez.
z = ez.
Tehtävä 355
Osoita, että pallokoordinaateille pätee
a)  r = er, b)
r = er, b) 
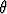 =
= 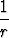 e
e , c)
, c) 
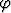 =
= 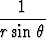 e
e .
.
Tehtävä 356
Totea oikeaksi seuraavat lieriökoordinaatteja koskevat kaavat:
a) 
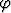 +
+  × (ln
× (ln 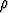
 z) = o, b)
z) = o, b)  ln
ln 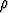 -
-  × (
× (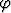
 z) = o.
z) = o.
Tehtävä 357
Totea oikeaksi seuraavat pallokoordinaatteja koskevat kaavat:
a)  × (cos
× (cos 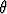

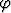 ) =
) = 
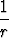 , b)
, b)  ×
× 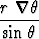 =
= 
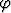 .
.
Tehtävä 358
Osoita, että lieriökoordinaattien yksikkövektoreiden osittaisderivaatat itse koordinaattien suhteen ovat = o paitsi
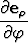 = e
= e ,
, 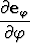 = -e
= -e .
.
Tehtävä 359
Laske pallokoordinaattien yksikkövektoreiden osittaisderivaatat itse koordinaattien suhteen ja esitä tulokset yksikkövektoreiden muodostamassa kannassa.Tehtävä 360
z-akselin ympäri kiertävän kentän vektorit ovat lieriökoordinaattien yksikkövektoreiden e suuntaiset ja niiden itseisarvo on suoraan verrannollinen z-akselista
lasketun etäisyyden neliöön. Laske kentän divergenssi ja roottori. Mitä nämä kertovat
kentästä?
suuntaiset ja niiden itseisarvo on suoraan verrannollinen z-akselista
lasketun etäisyyden neliöön. Laske kentän divergenssi ja roottori. Mitä nämä kertovat
kentästä?
Tehtävä 361
Virtauskentän kenttävektorit muodostuvat pallokoordinaattien yksikkövektoreista e . Laske kentän divergenssi ja roottori. Kuvaile, millaisesta
virtauksesta on kysymys. Missä sijaitsevat virtauksen lähteet?
. Laske kentän divergenssi ja roottori. Kuvaile, millaisesta
virtauksesta on kysymys. Missä sijaitsevat virtauksen lähteet?
Tehtävä 362
Laske pallokoordinaateissa r,
r, 
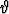 ja
ja 
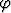 . Tulkitse saamasi tulos:
Minkä suuntaisia gradienttivektorit ovat? Osoita, että
. Tulkitse saamasi tulos:
Minkä suuntaisia gradienttivektorit ovat? Osoita, että  × (cos
× (cos 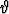

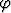 ) =
) = 
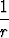 .
.
Tehtävä 363
Osoita, että kaavat
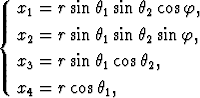
missä r > 0, 0 < 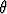 1 <
1 < 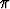 , 0 <
, 0 < 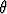 2 <
2 < 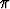 , 0 <
, 0 < 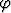 < 2
< 2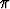 määrittelevät neliulotteiset
pallokoordinaatit. Miten on määriteltävä n-ulotteiset pallokoordinaatit?
määrittelevät neliulotteiset
pallokoordinaatit. Miten on määriteltävä n-ulotteiset pallokoordinaatit?