14 Pyörteettömät ja lähteettömät vektorikentät; potentiaali
14.1 Lähdekenttä ja pyörrekenttä
Tehtävä 407
Vektorikenttä määritellään lieriökoordinaateissa asettamalla
u(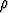 ,
, 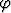 , z) =
, z) =  e
e .
.
Kuvaile, millainen kenttä on kyseessä. Laske sen divergenssi ja roottori. Mitä nämä kertovat kentästä?
Tehtävä 408
Pallosymmetrinen vektorikenttä määritellään yhtälöillä
u(r) = 
Laske kentän lähde- ja pyörrekenttä sekä vuo origokeskisen r-säteisen pallopinnan läpi.
Tehtävä 409
Osoita, että avaruuden kahdeksannes{ (x, y, z) | x > 0, y > 0, z > 0 }
on vektorikentän -
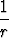 kenttäputki. Olkoon B mielivaltainen paloittain säännöllinen
putken poikkileikkauspinta. Laske kentän vuo pinnan B läpi.
kenttäputki. Olkoon B mielivaltainen paloittain säännöllinen
putken poikkileikkauspinta. Laske kentän vuo pinnan B läpi.
14.2 Pyörteetön vektorikenttä
Tehtävä 410
Todista, että xy-tason ympyrät x2 + y2 = 1 ja x2 + y2 - 4x = 5 ovat homotooppiset konstruoimalla sopiva kahden muuttujan jatkuva vektorifunktio, joka välittää muuntumisen.Tehtävä 411
Tutki, onko kaksiulotteisella vektorikentällä u(x, y) = (y + 2x)i + xj potentiaalia, ts. onko olemassa skalaarifunktiota V (x, y), jonka gradienttina kenttä saadaan. Laske potentiaali myönteisessä tapauksessa. Laske viivaintegraali
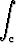 u . dr,
u . dr,
missä c on pisteitä (1, 0) ja (1, 2) yhdistävä origon kautta kulkeva ympyrän kaari.
Tehtävä 412
Määritä funktio g(y) siten, että tason vektorikentälläu(x, y) = 2xyg(y) i + x2(y + 1)g(y) j
on potentiaali.
Tehtävä 413
Valitse vakio c siten, että tason vektorikenttäu(x, y) = (x + cxy) i + x2 j
on pyörteetön. Määritä potentiaali, joka häviää pisteessä (1, 1). Laske valitsemallasi arvolla c viivaintegraali
 u . dr
u . dr
pisteitä P  (2a, -
(2a, -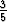 ) ja Q
) ja Q  (a,
(a, 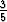 ) yhdistävää paloittain sileää tietä pitkin.
) yhdistävää paloittain sileää tietä pitkin.
Tehtävä 414
Osoita vektorikenttä u(x, y, z) = z i + z cos y j + (x + sin y) k pyörteettömäksi ja muodosta sen (skalaari)potentiaali.Tehtävä 415
Osoita seuraavat vektorikentät u(x, y, z) koko avaruudessa pyörteettömiksi ja etsi niiden skalaaripotentiaalit:| a) ex sin y i + ex cos y j + z k, | |||
| b) x i + z sin y j - cos y k, | |||
| c) 2xyz i + x2z j + x2y k, | |||
| d) (x2 + y2 + z2)(x i + y j + z k) = r2r, | |||
| e) - 2xe-y i + (x2e-y + sin z) j + y cos z k. |
Tehtävä 416
Miten funktio f(z) on valittava, jotta vektorikenttäu(x, y, z) = xy2 i + (cos z + x2y) j + yf(z) k
olisi pyörteetön koko avaruudessa? Määritä kentän potentiaali.
Tehtävä 417
Vektorikenttä
u(x, y, z) =  i +
i + 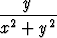 j
j
on määritelty koko avaruudessa z-akselia lukuunottamatta. Osoita, että se on pyörteetön ja konservatiivinen. Etsi potentiaali.
Tehtävä 418
Olkoon c puolitasossa { (x, y) | x > 0 } pisteitä (2, -2) ja (5, 0) yhdistävä paloittain sileä käyrä. Osoita, että tason viivaintegraali
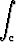 ln
ln 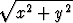 dx -
dx - 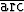 tan
tan  dy
dy
on tiestä c riippumaton ja laske sen arvo.
Tehtävä 419
Muodosta vektorikentälle
u(r) = 
fysikaalinen skalaaripotentiaali, so. etsi funktio V (r), jolle pätee u = - V . Normeeraa V
siten, että sen raja-arvo äärettömyydessä on = 0.
V . Normeeraa V
siten, että sen raja-arvo äärettömyydessä on = 0.
Tehtävä 420
Mikä ehto vakiovektoreiden a ja b on toteutettava, jotta kenttä u(r) = a(b . r) olisi pyörteetön? Osoita, että tällöin kentällä on potentiaali V (r) = - (a . r)(b . r).
(a . r)(b . r).
Tehtävä 421
Dipolin (kaksoislähteen) muodostaman vektorikentän potentiaali on
V (r) = 
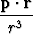 ,
,
missä p on vakiovektori. Laske kenttä ja sen lähdekenttä.
Tehtävä 422
Dipolin (kaksoislähteen) muodostaman vektorikentän potentiaali on
V (r) = 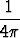
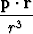 ,
,
missä p on vakiovektori. Laske kenttä. Piirrä potentiaalin tasa-arvokäyrät ja kenttä xy-tasossa, kun p = i + j.
Tehtävä 423
Jatkuvasti derivoituva vektorikenttä u ei ole pyörteetön, mutta kun se kerrotaan jatkuvasti derivoituvalla skalaarikentällä v saadaan pyörteetön kenttä vu. Osoita, että tällöin kentät u ja × u ovat kohtisuoria.
× u ovat kohtisuoria.
Tehtävä 424
Derivoituva skalaarikenttä v(r) toteuttaa yhtälön r . v = cv, missä c on
vakio. Mikä arvo tulee vakiolla c olla, jotta kenttä (
v = cv, missä c on
vakio. Mikä arvo tulee vakiolla c olla, jotta kenttä ( v × r) × r olisi konservatiivinen?
Määritä sen potentiaali.
v × r) × r olisi konservatiivinen?
Määritä sen potentiaali.
14.3 Lähteetön vektorikenttä
Tehtävä 425
Osoita vektorikenttä u(x, y, z) = x(z - y) i + y(x - z) j + z(y - x) k lähteettömäksi ja muodosta sen vektoripotentiaali.Tehtävä 426
Osoita seuraavat vektorikentät u(x, y, z) lähteettömiksi ja muodosta niiden vektoripotentiaalit:| a) xy i + j - yz k, | |||
| b) (z - y) i + (x - z) j + (y - x) k, | |||
| c) x2 i + (x2y - 2xy) j - x2z k, | |||
| d) (y + z) i + sin z j + cos x k. |
Tehtävä 427
Valitse funktio f(x, y, z) siten, että vektorikenttäu(x, y, z) = sin x i + cos y j + f(x, y, z) k
on lähteetön ja muodosta kentälle vektoripotentiaali.
Tehtävä 428
Määritä ne funktiot f(x), joilla kenttä u = f(x) rn r on lähteetön. Laske kentän vuo origoa ympäröivän umpinaisen pinnan läpi, kun n = -3 ja f(x) = 1 kaikilla x.Tehtävä 429
Määritä sellainen skalaarikenttä v(r) ja vektorikenttä A(r), että
 u +
u +  × A = x2y i + y2z j + z2x k.
× A = x2y i + y2z j + z2x k.
Onko vastaus yksikäsitteinen?
Tehtävä 430
Osoita alueessa G = 3 \ {(0, 0, 0)} määritelty vektorikenttä u(r) = r/r3
lähteettömäksi ja laske sen vuo origokeskisen pallopinnan läpi. Osoita Stokesin lauseen
avulla, että jos kentällä on vektoripotentiaali alueessa G, niin kentän vuot ylemmän ja
alemman puolipallon läpi ovat itseisarvoltaan yhtä suuret mutta vastakkaismerkkiset.
Mitä tästä voidaan päätellä vektoripotentiaalin suhteen?
3 \ {(0, 0, 0)} määritelty vektorikenttä u(r) = r/r3
lähteettömäksi ja laske sen vuo origokeskisen pallopinnan läpi. Osoita Stokesin lauseen
avulla, että jos kentällä on vektoripotentiaali alueessa G, niin kentän vuot ylemmän ja
alemman puolipallon läpi ovat itseisarvoltaan yhtä suuret mutta vastakkaismerkkiset.
Mitä tästä voidaan päätellä vektoripotentiaalin suhteen?
Tehtävä 431
Selosta vektorikentän pyörteettömyyden, lähteettömyyden, konservatiivisuuden, viivaintegraalin tiestä riippumattomuuden, skalaaripotentiaalin olemassaolon ja vektoripotentiaalin olemassaolon väliset yhteydet. Määritä avaruuden 3
vektorikentän u(x, y, z) = x i + y j + z k skalaaripotentiaali ja kentän v(x, y, z) = y i + x j
vektoripotentiaali.
3
vektorikentän u(x, y, z) = x i + y j + z k skalaaripotentiaali ja kentän v(x, y, z) = y i + x j
vektoripotentiaali.