![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Matemaattinen
induktio [ 1 2 ]
Matemaattinen
induktio [ 1 2 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) logiikka
logiikka
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Matemaattinen
induktio [ 1 2 ] Matemaattinen
induktio [ 1 2 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) logiikka logiikka
|
|
Olkoon P (n) jokin luonnollisesta luvusta n riippuva väittämä, joka halutaan osoittaa voimassa olevaksi, olipa n mikä tahansa luonnollinen luku.
Esimerkiksi P (n) voisi tarkoittaa yhtälöä
12 + 22 + ... + n2 =  n(n + 1)(2n + 1).
n(n + 1)(2n + 1).
Jos n = 5, kyseessä on yhtälö 12 + 22 + 32 + 42 + 52 =  . 5(5 + 1)(2 . 5 + 1);
merkintä P (5) tarkoittaa tätä yhtälöä. Arvolla n = 2 saadaan väittämä P (2) eli
12 + 22 =
. 5(5 + 1)(2 . 5 + 1);
merkintä P (5) tarkoittaa tätä yhtälöä. Arvolla n = 2 saadaan väittämä P (2) eli
12 + 22 =  . 2(2 + 1)(2 . 2 + 1). Arvolla n = 1 kutistuu väittämä P (1) muotoon
12 =
. 2(2 + 1)(2 . 2 + 1). Arvolla n = 1 kutistuu väittämä P (1) muotoon
12 =  . 1(1 + 1)(2 . 1 + 1). Kaikki nämä ovat voimassa olevia yhtälöitä, kuten
yksinkertaiset laskut osoittavat.
. 1(1 + 1)(2 . 1 + 1). Kaikki nämä ovat voimassa olevia yhtälöitä, kuten
yksinkertaiset laskut osoittavat.
Yhtälö on voimassa joka ainoalle luonnolliselle luvulle n, ts. P (n) on tosi kaikilla n, mutta muutamien arvojen kokeilu ei tietenkään riitä todistamaan tätä.
Matemaattinen induktio on todistusmenetelmä, jota voidaan käyttää tämäntyyppisten asioiden todistamiseen.
Todistuksen rakenne on seuraava:
1) Osoitetaan aluksi, että väittämä P (1) on tosi. Tämä on yleensä yksinkertainen lasku.
2) Todistetaan ns. induktioaskel: Jos P (n) on tosi, niin myös P (n + 1) on tosi eli
symbolein P (n) 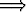 P (n + 1). Tämä todistus on suoritettava siten, että päättely
on pätevä kaikille luonnollisille luvuille n.
P (n + 1). Tämä todistus on suoritettava siten, että päättely
on pätevä kaikille luonnollisille luvuille n.
Tällöin katsotaan väittämän P (n) tulleen todistetuksi kaikille arvoille n 
 .
Perusteluna on seuraavan ketjun syntyminen:
.
Perusteluna on seuraavan ketjun syntyminen:
P (1)  P (2)
P (2)  P (3)
P (3) 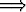 P (4)
P (4) 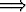 ....
....
Aluksi on nimittäin todettu P (1) voimassa olevaksi. Koska induktioaskel on
todistettu jokaiselle arvolle n, se pätee erityisesti arvolla n = 1: jos P (1) on tosi,
niin myös P (2) on. Mutta P (1) on jo osoitettu todeksi ja siis myös P (2) on
tosi. Arvolla n = 2 induktioaskel antaa P (2)  P (3). Koska edellä
on jo P (2) osoitettu todeksi, seuraa tästä, että myös P (3) on tosi. Näin
jatketaan.
P (3). Koska edellä
on jo P (2) osoitettu todeksi, seuraa tästä, että myös P (3) on tosi. Näin
jatketaan.
Induktiotodistuksen alkukohdan ei välttämättä tarvitse olla n = 1, vaan aivan hyvin voidaan aloittaa jostakin muustakin arvosta n = n0 ja samalla periaatteella osoittaa väittämä päteväksi arvoilla n > n0.
![[#]](kuvat/msam10-c-4.gif) luonnollinen luku luonnollinen luku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12