 . Jos ellipsin keskipiste
. Jos ellipsin keskipiste  on origossa ja polttopisteiksi
valitaan
on origossa ja polttopisteiksi
valitaan 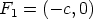 ja
ja  , ellipsin yhtälö on
, ellipsin yhtälö on
Ellipsin muodostavat ne pisteet, joilla kahdesta kiinteästä pisteestä —
polttopisteistä — laskettujen etäisyyksien summa on vakio. Vakion arvoksi
merkitään yleensä  . Jos ellipsin keskipiste
. Jos ellipsin keskipiste  on origossa ja polttopisteiksi
valitaan
on origossa ja polttopisteiksi
valitaan 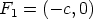 ja
ja  , ellipsin yhtälö on
, ellipsin yhtälö on

missä 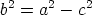 .
.
Ellipsi voidaan piirtää asettamalla polttopisteet  ja
ja 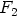 keskipisteinä kaksi
ympyrää, joiden säteiden summa on
keskipisteinä kaksi
ympyrää, joiden säteiden summa on  . Ympyröiden leikkauspisteet ovat ellipsin
pisteitä. Kaikki ellipsin pisteet saadaan varioimalla ympyröiden säteitä siten, että
niiden summa pysyy vakiona.
. Ympyröiden leikkauspisteet ovat ellipsin
pisteitä. Kaikki ellipsin pisteet saadaan varioimalla ympyröiden säteitä siten, että
niiden summa pysyy vakiona.
Applet created on 04.07.2005 by SKK with CabriJava
Oheinen kuvio on laadittu Cabri-Geometria-ohjelmalla. Cabri-dokumentissa
voidaan ympyröiden säteitä muuttaa siirtämällä hiirellä alareunassa olevan janan
keskellä sijaitsevaa säätöpistettä  . Tällöin säteiden summa säilyy vakiona
. Tällöin säteiden summa säilyy vakiona
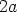 (= janan pituus), mutta säteiden pituudet muuttuvat. Ympyröiden
leikkauspisteet
(= janan pituus), mutta säteiden pituudet muuttuvat. Ympyröiden
leikkauspisteet 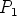 ja
ja 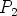 piirtävät tällöin ellipsin ylemmän ja alemman kaaren
ja
piirtävät tällöin ellipsin ylemmän ja alemman kaaren
ja  . Kaaret saadaan näkyviin asettamalla
Cabrin trace-toiminto päälle.
. Kaaret saadaan näkyviin asettamalla
Cabrin trace-toiminto päälle.
Piste 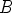 on säätöpiste, jota siirtämällä voidaan muuttaa ellipsin eksentrisyyttä,
ts. polttopisteiden
on säätöpiste, jota siirtämällä voidaan muuttaa ellipsin eksentrisyyttä,
ts. polttopisteiden  ja
ja 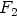 etäisyyttä keskipisteestä
etäisyyttä keskipisteestä 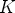 . Itse asiassa
. Itse asiassa  on
ellipsin pikku akselin päätepiste.
on
ellipsin pikku akselin päätepiste.
Harjoitustehtäviä
Linkkejä
Vastaava Cabri-dokumentti
Cabri-ohjeet
Simo K. Kivelä 10.02.2004