Ellipsin piirtäminen pisteittäin
Yksinkertaisia geometrisia konstruktioita, joilla ellipsi voidaan muodostaa
pisteittäin, on paljon. Seuraavassa esitettävällä on läheinen yhteys ellipsille
yleensä käytettävään parametriesitykseen.
Olkoon annettuna kaksi samankeskistä ympyrää. Näiden säteet ovat
muodostettavan ellipsin puoliakseleiden pituudet. Olkoon lisäksi annettuna
kaksi toisiaan vastaan kohtisuoraa suuntaa. Nämä määräävät ellipsin
akseleiden suunnat. Seuraavassa näitä kutsutaan vaaka- ja pystysuoriksi
suunniksi.
Ympyröiden yhteisestä keskipisteestä  lähtevä säde leikatkoon ympyrät
pisteissä
lähtevä säde leikatkoon ympyrät
pisteissä 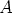 ja
ja  . Asetetaan pisteen
. Asetetaan pisteen 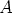 kautta pystysuora ja pisteen
kautta pystysuora ja pisteen  kautta
vaakasuora suora; näiden leikkauspiste olkoon
kautta
vaakasuora suora; näiden leikkauspiste olkoon 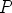 . Kun säde kiertää täyden
kierroksen, piirtää piste
. Kun säde kiertää täyden
kierroksen, piirtää piste  ellipsin. Pienempi ympyröistä sivuaa ellipsiä
sisäpuolisesti, suurempi ulkopuolisesti.
ellipsin. Pienempi ympyröistä sivuaa ellipsiä
sisäpuolisesti, suurempi ulkopuolisesti.
Applet created on 30.12.2004 by SKK with
CabriJava
Olkoon ympyröiden keskipiste origo, ymyröiden säteet  ja
ja 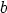 (
(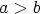 ) ja säteen
suuntakulma
) ja säteen
suuntakulma 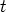 . Tällöin on suorakulmaisten kolmioiden trigonometrialla
nähtävissä, että pisteen
. Tällöin on suorakulmaisten kolmioiden trigonometrialla
nähtävissä, että pisteen 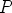 koordinaatit ovat
koordinaatit ovat

Tämä on yleisesti käytetty ellipsin parametriesitys. Säteen suuntakulmaa
 kutsutaan myös eksentriseksi anomaliaksi. Koko ellipsi saadaan, kun
kutsutaan myös eksentriseksi anomaliaksi. Koko ellipsi saadaan, kun
 .
.
Eo. kuvio on laadittu Cabri-Geometria-ohjelmalla. Cabri-dokumentissa voidaan
pistettä  hiirellä siirtämällä kääntää sädettä
hiirellä siirtämällä kääntää sädettä  , jolloin piste
, jolloin piste 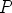 liikkuu
vastaavasti. Pisteen
liikkuu
vastaavasti. Pisteen 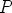 ura saadaan näkyviin panemalla Cabrin trace-toiminto
päälle.
ura saadaan näkyviin panemalla Cabrin trace-toiminto
päälle.
Harjoitustehtäviä
Osoita, että syntyvä käyrä todella on ellipsi. Tutki, miten ympyröiden säteiden
muuttaminen vaikuttaa ellipsin muotoon. Millainen ellipsi saadaan, jos
konstruktiota muutetaan siten, että pisteen  kautta asetetaan vaakasuora ja
pisteen
kautta asetetaan vaakasuora ja
pisteen 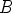 kautta pystysuora suora?
kautta pystysuora suora?
Linkkejä
Vastaava Cabri-dokumentti
Cabri-ohjeet
Simo K. Kivelä 11.02.2004
 lähtevä säde leikatkoon ympyrät
pisteissä
lähtevä säde leikatkoon ympyrät
pisteissä 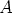 ja
ja  . Asetetaan pisteen
. Asetetaan pisteen 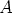 kautta pystysuora ja pisteen
kautta pystysuora ja pisteen  kautta
vaakasuora suora; näiden leikkauspiste olkoon
kautta
vaakasuora suora; näiden leikkauspiste olkoon 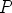 . Kun säde kiertää täyden
kierroksen, piirtää piste
. Kun säde kiertää täyden
kierroksen, piirtää piste  ellipsin. Pienempi ympyröistä sivuaa ellipsiä
sisäpuolisesti, suurempi ulkopuolisesti.
ellipsin. Pienempi ympyröistä sivuaa ellipsiä
sisäpuolisesti, suurempi ulkopuolisesti.
 ja
ja 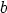 (
(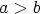 ) ja säteen
suuntakulma
) ja säteen
suuntakulma 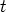 . Tällöin on suorakulmaisten kolmioiden trigonometrialla
nähtävissä, että pisteen
. Tällöin on suorakulmaisten kolmioiden trigonometrialla
nähtävissä, että pisteen 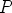 koordinaatit ovat
koordinaatit ovat

 kutsutaan myös
kutsutaan myös  .
.
 hiirellä siirtämällä kääntää sädettä
hiirellä siirtämällä kääntää sädettä  , jolloin piste
, jolloin piste 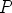 liikkuu
vastaavasti. Pisteen
liikkuu
vastaavasti. Pisteen 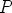 ura saadaan näkyviin panemalla Cabrin trace-toiminto
päälle.
ura saadaan näkyviin panemalla Cabrin trace-toiminto
päälle.
 kautta asetetaan vaakasuora ja
pisteen
kautta asetetaan vaakasuora ja
pisteen 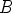 kautta pystysuora suora?
kautta pystysuora suora?